
【题目】已知直线l1:y=﹣![]() 与直线l2:y=kx﹣
与直线l2:y=kx﹣![]() 交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
交于x轴上的同一个点A,直线l1与y轴交于点B,直线l2与y轴的交点为C.
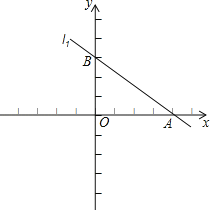
(1)求k的值,并作出直线l2图象;
(2)若点P是线段AB上的点且△ACP的面积为15,求点P的坐标;
(3)若点M、N分别是x轴上、线段AC上的动点(点M不与点O重合),是否存在点M、N,使得△ANM≌△AOC?若存在,请求出N点的坐标;若不存在,请说明理由.
【答案】(1)k=![]() ,见解析;(2)点P的坐标(
,见解析;(2)点P的坐标(![]() ,
,![]() );(3)当N的纵坐标为(
);(3)当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.
【解析】
试题分析:(1)对于直线l1,令y=0求出x的值,确定出A坐标,代入直线l2求出k的值,作出直线l2图象即可;
(2)设P(a,b),△ACP面积=△ABC面积﹣△BPC面积,根据已知三角形ACP面积求出a的值,进而求出b的值,确定出P坐标即可;
(3)如图2,作ND⊥x轴于D,利用勾股定理求出AC的长,由△ANM≌△AOC,得到对应边相等,表示出AM,AN,MN,确定出△AMN为直角三角形,利用面积法求出ND的长,确定出N纵坐标,进而求出横坐标,确定出N坐标即可.
解:(1)∵直线l1:y=﹣![]() x+3与x轴交于点A,
x+3与x轴交于点A,
∴令y=0时,x=4,即A(4,0),
将A(4,0)代入直线l2:y=kx﹣![]() ,得k=
,得k=![]() ,
,
直线l2图象如图1所示;
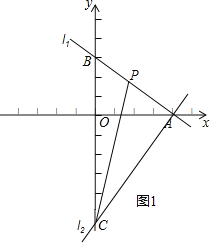
(2)设P(a,b),
根据题意得:S△ACP=S△ABC﹣S△PBC=![]() ×(3+
×(3+![]() )×4﹣
)×4﹣![]() ×(3+
×(3+![]() )a=15,
)a=15,
解得:a=![]() ,
,
将P(![]() ,b)代入直线l1得:b=
,b)代入直线l1得:b=![]() ×(﹣
×(﹣![]() )+3=﹣
)+3=﹣![]() +3=
+3=![]() ,
,
∴点P的坐标(![]() ,
,![]() );
);
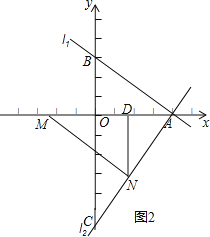
(3)如图2,作ND⊥x轴于D,
∵AC=![]() =
=![]() ,△ANM≌△AOC,
,△ANM≌△AOC,
∴AM=AC=![]() ,AN=AO=4,MN=OC=
,AN=AO=4,MN=OC=![]() ,∠ANM=∠AOC=90°,
,∠ANM=∠AOC=90°,
∵S△AMN=![]() AMND=
AMND=![]() ANMN,
ANMN,
∴ND=![]() =
=![]() =
=![]() ,
,
将N的纵坐标y=﹣![]() 代入直线l2得:x=
代入直线l2得:x=![]() ,
,
∴当N的纵坐标为(![]() ,﹣
,﹣![]() )时,△ANM≌△AOC.
)时,△ANM≌△AOC.


科目:初中数学 来源: 题型:
【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD.
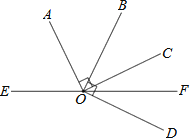
(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
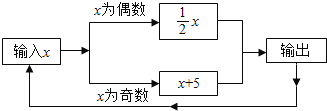
【题目】有一数值转换机,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是 ,依次继续下去…,第2015次输出的结果是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数轴上A、B两点表示的有理数分别为a、b,且(a﹣1)2+|b+2|=0,
(1)求(a+b)2015的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述实验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC交CE的延长线于F.

(1)求证:△ACD≌△CBF;
(2)求证:AB垂直平分DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com