

分析 (1)只要证明∠AIB=90°+$\frac{1}{2}$∠ACB,∠ADI=90°+$\frac{1}{2}$∠ACB即可;
(2)①只要证明∠IDC=∠DCF即可;
②首先求出∠ACE-∠ABC=∠BAC=70°,再证明∠F=$\frac{1}{2}$∠ACE-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACE-∠ABC)即可解决问题;
解答 (1)证明:∵AI、BI分别平分∠BAC,∠ABC,
∴∠BAI=$\frac{1}{2}$∠BAC,∠ABI=$\frac{1}{2}$∠ABC,
∴∠BAI+∠ABI=$\frac{1}{2}$(∠BAC+∠ABC)=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∴在△ABI中,∠AIB=180°-(∠BAI+∠ABI)
=180°-(90°-$\frac{1}{2}$∠ACB)
=90°+$\frac{1}{2}$∠ACB,
∵CI平分∠ACB,
∴∠DCI=$\frac{1}{2}$∠ACB,
∵DI⊥IC,
∴∠DIC=90°,
∴∠ADI=∠DIC+∠DCI=90°+$\frac{1}{2}$∠ACB,
∴∠AIB=∠ADI.
(2)①解:结论:DI∥CF.
理由:∵∠IDC=90°-∠DCI=90°-$\frac{1}{2}$∠ACB,
∵CF平分∠ACE,
∴∠ACF=$\frac{1}{2}$∠ACE=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∴∠IDC=∠ACF,
∴DI∥CF.
②解:∵∠ACE=∠ABC+∠BAC,
∴∠ACE-∠ABC=∠BAC=70°,
∵∠FCE=∠FBC+∠F,
∴∠F=∠FCE-∠FBC,
∵∠FCE=$\frac{1}{2}$∠ACE,∠FBC=$\frac{1}{2}$∠ABC,
∴∠F=$\frac{1}{2}$∠ACE-$\frac{1}{2}$∠ABC=$\frac{1}{2}$(∠ACE-∠ABC)=35°
点评 本题考查三角形的内角和定理、三角形的外角的性质、平行线的判定等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{25}$的平方根是±$\frac{1}{5}$ | B. | -9是81的一个平方根 | ||
| C. | 0.2的算术平方根是0.01 | D. | -27的立方根是-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 抛掷次数n | 100 | 200 | 300 | 400 | 600 | 800 | 1000 |
| 针尖不着地的频数m | 64 | 118 | 189 | 252 | 360 | 488 | 610 |
| 针尖不着地的频数$\frac{m}{n}$ | 0.64 | 0.59 | 0.63 | 0.63 | 0.60 | 0.61 | 0.61 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
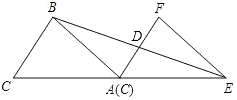 如图,在△ABC中,AB=AC,将△ABC沿射线CA方向平移,平移后顶点C到达点A处,得到△EFA.
如图,在△ABC中,AB=AC,将△ABC沿射线CA方向平移,平移后顶点C到达点A处,得到△EFA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
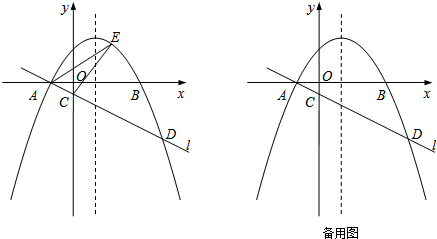
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | -2a<-2b | C. | 0.7a<0.7b | D. | -$\frac{a}{4}$$>-\frac{b}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com