
分析 先把二元二次方程进行因式分解,再把②代入,求出$\sqrt{5}$x+2y的值,再与②相加减,求出方程组的解.
解答 解:$\left\{\begin{array}{l}{5{x}^{2}-4{y}^{2}=20①}\\{\sqrt{5}x-2y=2\sqrt{15}②}\end{array}\right.$
由①得,($\sqrt{5}$x+2y)($\sqrt{5}$x-2y)=20,
∴$\sqrt{5}$x+2y=$\frac{2}{3}\sqrt{15}$③
③+②得,x=$\frac{4}{3}\sqrt{3}$
③-②得,y=-$\frac{\sqrt{15}}{3}$
所以方程组的解为:$\left\{\begin{array}{l}{x=\frac{4}{3}\sqrt{3}}\\{y=-\frac{\sqrt{15}}{3}}\end{array}\right.$
点评 本题考查的是二元二次方程组的解法,把二元二次方程正确进行因式分解是解题的关键,注意整体代入法的运用.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
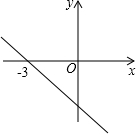 一次函数与方程、不等式的关系
一次函数与方程、不等式的关系查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
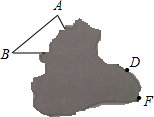 平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.
平移△ABC,使得边AB移到DE的位置,如图是小刚的作业,他的作法完全正确.可由于一不小心将一团墨汁沾染到了作业本上,请设法帮小刚补全平移前后的△ABC和△DEF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com