
 如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆的矩形花圃.
如图,有长为24m的篱笆,一面利用墙(墙的最大可用长度为10m),围成中间隔有一道篱笆的矩形花圃.分析 (1)设花圃的宽AB为xm,长就为(24-3x)m,根据矩形的面积公式列出方程,解方程得出x的值后根据墙的最大可用长度为10m取舍可得;
(2)设矩形花圃的面积为y,根据矩形的面积公式列出函数解析式,利用二次函数的性质结合自变量x的范围求出最大值即可得.
解答 解:(1)设花圃的宽AB为xm,长就为(24-3x)m,由题意得
(24-3x)x=45,
解得:x=3或x=5,
当x=3时,24-3x=15>10,舍去,
当x=5时,24-3x=9<10,符合题意,
答:若要围成面积为45m2的花圃,AB的长是5米;
(2)设矩形花圃的面积为y,
则y=x(24-3x)=-3x2+24x=-3(x-4)2+48,
∵24-3x≤10,
解得x≥$\frac{14}{3}$,
∴当x>4时,y随x的增大而减小,
∴当x=$\frac{14}{3}$时,ymax=46,
答:能围成面积比45m2更大的花圃,当AB的长为$\frac{14}{3}$时,面积最大,最大面积为46m2.
点评 本题主要考查二次函数的应用,根据矩形的面积公式列出方程和二次函数的解析式,并熟练掌握二次函数的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=(x+1)2-2 | B. | y=(x-1)2-2 | C. | y=(x-1)2+2 | D. | y=(x+1)2-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
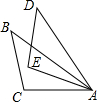 如图,下列条件中,不能证明△ABC≌△ADE的是( )
如图,下列条件中,不能证明△ABC≌△ADE的是( )| A. | ∠B=∠D,∠C=∠E,AC=AE | B. | AB=AD,∠B=∠D,BC=DE | ||
| C. | AC=AE,AB=AD,∠B=∠D | D. | AC=AE,BC=DE,AB=AD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com