6
分析:要求CE的长,应先设CE的长为x,由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AD
1E,所以AD
1=10cm,ED
1=DE=8-x;在Rt△ABD
1中由勾股定理得:
AB
2+BD
12=AD
12,已知AB、AD
1的长可求出BD
1的长,又CD
1=BC-BD
1=10-BD
1,在Rt△ECD
1中由勾股定理可得:ED
12=CE
2+CD
12,即:(8-x)
2=x
2+(10-BD
1)
2,将求出的BD
1的值代入该方程求出x的值,则求出了CE的长,进而求出面积即可.
解答:∵四边形ABCD是矩形,
∴AD=BC=10cm,CD=AB=8cm,
根据题意得:Rt△ADE≌Rt△AD
1E,
∴∠AD
1E=90°,AD
1=10cm,ED
1=DE,
设CE=xcm,则DE=ED
1=CD-CE=8-x,
在Rt△ABD
1中由勾股定理得:AB
2+BD
12=AD
12,
即8
2+BD
12=10
2,
∴BD
1=6cm,
∴CD
1=BC-BD
1=10-6=4(cm),
在Rt△ECF中由勾股定理可得:ED
12=CE
2+CD
12,
即(8-x)
2=x
2+4
2,
∴64-16x+x
2=x
2+16,
∴x=3(cm),
即CE=3cm.
故

×3×4=6.
故答案为:6.
点评:本题主要考查运用勾股定理、全等三角形、方程思想等知识,根据已知条件求出三角形的边长是解题关键.

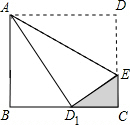 已知长方形的长AD=10,AB=8,将它沿着AE折叠,使得D点恰好落在BC边上,则
已知长方形的长AD=10,AB=8,将它沿着AE折叠,使得D点恰好落在BC边上,则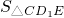 =________.
=________. ×3×4=6.
×3×4=6.

 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案