
【题目】已知13 = 1 =![]() ×12×22, 13+23=9=
×12×22, 13+23=9=![]() ×22×32,13 + 23 + 33 = 36 =
×22×32,13 + 23 + 33 = 36 =![]() ×32×42, …,按照这个规律完成下列问题:
×32×42, …,按照这个规律完成下列问题:
(1)13+23+33+43+53=________=![]() × ( )2 × ( )2
× ( )2 × ( )2
(2)猜想:13+23+33+…+n3=___________
(3)利用(2)中的结论计算:(写出计算过程)
113+123 + 313+143 + 153+163 + ……+393+403.
科目:初中数学 来源: 题型:
【题目】阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: ![]() .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: ![]() ,
, ![]() 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: ![]() ,
, ![]() 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: ![]() ;
; ![]() ;
;
再如: ![]() .
.
解决下列问题:
(1)分式![]() 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式![]() 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式![]() 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某开发商进行商铺促销,广告上写着如下条款:投资者购买商铺后,必须由开发商代租赁5年,5年期满后由开发商以比原商铺标价高20%的价格进行回购,投资者可在以下两种购铺方案中做出选择:
方案一:按照商铺标价一次性付清铺款,每年可获得的租金为商铺标价的10%;
方案二:按商铺标价的八折一次性付清铺款,前3年商铺的租金收益归开发商所有,3年后每年可获得的租金为商铺标价的9%
(1)问投资者选择哪种购铺方案,5年后所获得的投资收益率更高?为什么?
(注:投资收益率=![]() ×100%)
×100%)
(2)对同一标价的商铺,甲选择了购铺方案一,乙选择了购铺方案二,那么5年后两人获得的收益相差7.2万元.问甲乙两人各投资了多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC的外侧作直线AP,点C关于直线AP的对称点为点D,连接AD,BD,其中BD交直线AP于点E.
(1)依题意补全图形;(2)若∠PAC=20°,求∠AEB的度数;
(3)连结CE,写出AE, BE, CE之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
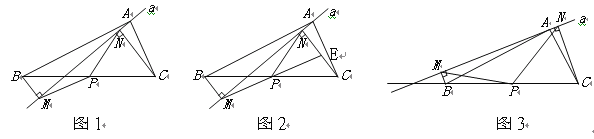
【题目】如图1,在△ABC中,点P为BC边中点,直线a绕顶点A旋转,若B、P在直线a的异侧,BM直线a于点M,CN直线a于点N,连接PM、PN;
(1) 延长MP交CN于点E(如图2)。求证:△BPM≌△CPE;求证:PM=PN;
(2) 若直线a绕点A旋转到图3的位置时,点B、P在直线a的同侧,其它条件不变。此时
PM=PN还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3) 若直线a绕点A旋转到与BC边平行的位置时,其它条件不变。请直接判断四边形MBCN
的形状及此时PM=PN还成立吗?不必说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四人做传数游戏,甲任报一个数给乙,乙把这个数加1传给丙,丙再把所得的数平方后传给丁,丁把所听到的数减1报出答案.若甲报的数为﹣9,则丁的答案是( )
A.63B.52C.30D.﹣17
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速铁路工程指挥部,要对某路段工程进行招标,接到了甲、乙两个工程队的投标书.从投标书中得知:甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的![]() :若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
:若由甲队先做20天,剩下的工程再由甲、乙两队合作60天完成.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)已知甲队每天的施工费用为8.6万元,乙队每天的施工费用为5.4万元,工程预算的施工费用为1000万元.若在甲、乙工程队工作效率不变的情况下使施工时间最短,问拟安排预算的施工费用是否够用?若不够用,需追加预算多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个多边形的所有内角与它的一个外角之和是2018°,求这个外角的度数和它的边数.
【答案】38° ; 边数13
【解析】试题分析:根据多边形的内角和公式(n-2)180°可知,多边形的内角和是180°的倍数,然后列式求解即可.
试题解析:设多边形的边数是n,加的外角为α,则
(n-2)180°+α=2018°,
α=2378°-180°n,又0<α<180°,
即0<2378°-180°n<180°,
解得: ![]() <n<
<n<![]() ,
,
又n为正整数,
可得n=13,
此时α=38°满足条件,
答:这个外角的度数是38°,它的13边形.
【点睛】本题考查了多边形的内角和公式,利用好多边形的内角和是180°的倍数是解题的关键.
【题型】解答题
【结束】
22
【题目】已知![]() , 求 (1)
, 求 (1) ![]() ; (2)
; (2) ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com