
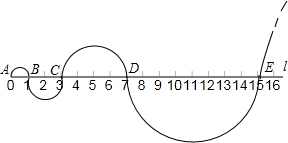
 如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π)
如图,在你标有刻度的直线l上,从点A开始,以AB=1为直径画半圆,记为第1个半圆;以BC=2为直径画半圆,记为第2个半圆;以CD=4为直径画半圆,记为第3个半圆;以DE=8为直径画半圆,记为第4个半圆…,按此规律,则第4个半圆的面积是第3个半圆面积的4倍,第n个半圆的面积为22n-5π.(结果保留π) 分析 根据已知图形得出第4个半圆的半径和第3个半圆的半径,进而得出第4个半圆的面积与第3个半圆面积的关系,得出第n个半圆的半径,进而得出答案.
解答 解:∵以AB=1为直径画半圆,记为第1个半圆;
以BC=2为直径画半圆,记为第2个半圆;
以CD=4为直径画半圆,记为第3个半圆;
以DE=8为直径画半圆,记为第4个半圆,
∴第4个半圆的面积为:$\frac{π×{4}^{2}}{2}$=8π,
第3个半圆面积为:$\frac{π×{2}^{2}}{2}$=2π,
∴第4个半圆的面积是第3个半圆面积的$\frac{8π}{2π}$=4倍;
根据已知可得出第n个半圆的直径为:2n-1,
则第n个半圆的半径为:$\frac{{2}^{n-1}}{2}={2}^{n-2}$,
第n个半圆的面积为:$\frac{π×({2}^{n-2})^{2}}{2}={2}^{2n-5}π$.
故答案为:4,22n-5π.
点评 此题主要考查了数字变化规律,注意数字之间变化规律,根据已知得出第n个半圆的直径为:2n-1是解题关键.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:解答题
| 射击成绩(环) | 6 | 7 | 8 | 9 | 10 |
| 甲射击频数 | 0 | 3 | 4 | 3 | 0 |
| 乙射击频数 | 1 | 3 | 2 | 3 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
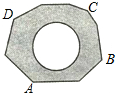 如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下:
如图,地面上有一个不规则的封闭图形ABCD,为求得它的面积,小明在此封闭图形内画出一个半径为1米的圆后,在附近闭上眼睛向封闭图形内掷小石子(可把小石子近似地看成点),记录如下: | 50 | 50 | 300 | … |
| 石子落在圆内(含圆上)次数m | 14 | 48 | 89 | … |
| 石子落在圆以外的阴影部分(含外缘上)次数n | 30 | 95 | 180 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:
如图,在△ABC中,D、E分别是AB、AC上的点,DC交BE于F,且AD:AB=1:3,AE=$\frac{1}{2}$EC,求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | $\sqrt{23}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com