
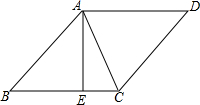
 如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )
如图,在菱形ABCD中,AB=5,对角线AC=6,过A作AE⊥BC,垂足为E,则AE的长是( )| A. | 24 | B. | 36 | C. | 48 | D. | 4.8 |
分析 连接BD,根据菱形的性质可得AC⊥BD,AO=$\frac{1}{2}$AC,然后根据勾股定理计算出BO长,再算出菱形的面积,然后再根据面积公式BC•AE=$\frac{1}{2}$AC•BD可得答案.
解答 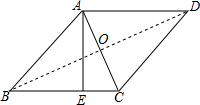 解:连接BD,交AC于O点,
解:连接BD,交AC于O点,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5,
∴AC⊥BD,AO=$\frac{1}{2}$AC,BD=2BO,
∴∠AOB=90°,
∵AC=6,
∴AO=3,
∴B0=$\sqrt{25-9}$=4,
∴DB=8,
∴菱形ABCD的面积是$\frac{1}{2}$×AC•DB=$\frac{1}{2}$×6×8=24,
∴BC•AE=24,
AE=4.8,
故选:D.
点评 此题主要考查了菱形的性质,以及菱形的性质面积,关键是掌握菱形的对角线互相垂直且平分.


科目:初中数学 来源: 题型:填空题
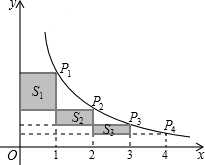 如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.
如图,在反比例函数$y=\frac{k}{x}$(x>0)的图象上有点P1,P2,P3,P4,它们的横坐标依次为1,2,3,4.分别过这些点作x轴和y轴的垂线.图中所构成的阴影部分面积从左到右依次为S1,S2,S3,若S1+S2+S3=2.4,则k的值为3.2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -4或6 | C. | 6或1 | D. | 1或-4或6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
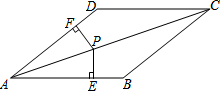 如图,在四边形ABCD中,AB∥CD,∠B=∠D.
如图,在四边形ABCD中,AB∥CD,∠B=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总个数 | |
| 甲班 | 89 | 100 | 98 | 110 | 103 | 500 |
| 乙班 | 100 | 89 | 97 | 119 | 95 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com