
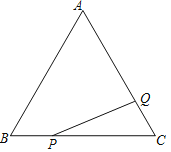
【题目】如图,已知等边△ABC的边长为4,点P,Q分别是边BC,AC上一点,PB=1,则PA=_____,若BQ=AP,则AQ=_____.
【答案】![]() 3
3
【解析】
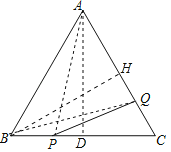
连接AP,过A作AD⊥BC于D,根据等边三角形的性质得到BD=CD=![]() BC=
BC=![]() 4=2,∠BAD=30°,根据含30°直角三角形的性质以及勾股定理可得出PA的长;连接BQ,过B作BH⊥AC于H,先根据等边三角形的性质可得出AH的长,在Rt△BHQ中,根据勾股定理可求出HQ的长,从而可得出结果.
4=2,∠BAD=30°,根据含30°直角三角形的性质以及勾股定理可得出PA的长;连接BQ,过B作BH⊥AC于H,先根据等边三角形的性质可得出AH的长,在Rt△BHQ中,根据勾股定理可求出HQ的长,从而可得出结果.
解:连接AP,过A作AD⊥BC于D,
∵△ABC是等边三角形,
∴BD=CD=![]() BC=
BC=![]() 4=2,∠BAD=30°,
4=2,∠BAD=30°,
∴BD=![]() AB,∴AD=
AB,∴AD=![]() AB=2
AB=2![]() ,
,
∵PB=1,∴PD=1,
∴PA=![]() =
=![]() =
=![]() ;
;
连接BQ,过B作BH⊥AC于H,
∴AH=![]() AC=2,
AC=2,
∴BH=AD=2![]() ,
,
∴HQ=![]() =
=![]() =1,
=1,
∴AQ=AH+HQ=3,
故答案为:![]() ;3.
;3.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
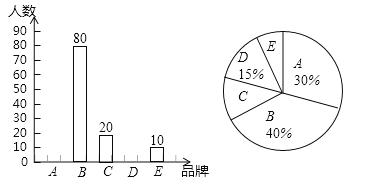
【题目】“共享单车,绿色出行”,现如今骑共享单车出行不但成为一种时尚,也称为共享经济的一种新形态,某校九(1)班同学在街头随机调查了一些骑共享单车出行的市民,并将他们对各种品牌单车的选择情况绘制成如下两个不完整的统计图(A:摩拜单车;B:ofo单车;C:HelloBike).请根据图中提供的信息,解答下列问题:
(1)求出本次参与调查的市民人数;
(2)将上面的条形图补充完整;
(3)若某区有10000名市民骑共享单车出行,根据调查数据估计该区有多少名市民选择骑摩托单车出行?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“太原市批发市场”与“西安市批发市场”之间的商业往来频繁, 如图,“太原市批发市场”“西安市批发市场”与“长途汽车站”在同一线路上,每天中午12:00一辆客车由“太原市批发市场”驶往“长途汽车站”,一辆货车由“西安市批发市场”驶往“太原市批发市场”,假设两车同时出发,匀速行驶,图2分别是客车、货车到“长途汽车站”的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图像.
之间的函数图像.
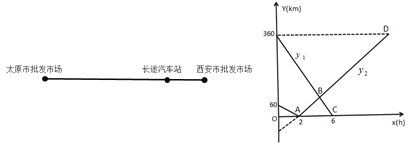
请你根据图象信息解决下列问题:
(1)由图 2 可知客车的速度为 km/h,货车的速度为 km/h;
(2)根据图 2 直接写出直线 BC 的函数关系式为 ,直线 AD 的函数关系式为 ;
(3)求点B的坐标,并解释点B的实际意义.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB≌△ADC,点B和点C是对应顶点,∠O=∠D=90°,记∠OAD=α,∠ABO=β,当BC∥OA时,α与β之间的数量关系为( )
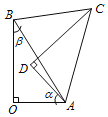
A.α=βB.α=2βC.α+β=90°D.α+β=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(知识背景)我国古代把直角三角形较短的直角边称为“勾”,较长的的直角边称为“股”,斜边称为“弦”.据《周髀算经》记载,公元前1000多年就发现了“勾三股四弦五”的结论.像3、4、5这样为三边长能构成直角三角形的3个正整数,称为勾股数.
(应用举例)
观察3,4,5;5,12,13;7,24,25;![]()
可以发现这些勾股数的勾都是奇数,且从3起就没有间断过,
当勾为3时,股![]() ,弦
,弦![]() ;
;
当勾为5时,股![]() ,弦
,弦![]() ;
;
当勾为7时,股![]() ,弦
,弦![]() .
.
请仿照上面三组样例,用发现的规律填空:
(1)如果勾用![]() ,且
,且![]() 为奇数)表示时,请用含有
为奇数)表示时,请用含有![]() 的式子表示股和弦,则股
的式子表示股和弦,则股![]() ,弦
,弦![]() .
.
(问题解决)
(2)古希腊的哲学家柏拉图也提出了构造勾股数组的公式.具体表述如下:如果![]() ,
,![]() ,
,![]() 为大于1的整数),则
为大于1的整数),则![]() 、
、![]() 、
、![]() 为勾股数.请你证明柏拉图公式的正确性;
为勾股数.请你证明柏拉图公式的正确性;
(3)毕达哥拉斯在他找到的勾股数的表达式中发现弦与股的差为1,若用![]() 为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
为任意正整数)表示勾股数中最大的一个数,请你找出另外两个数的表达式分别是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠ABC=90o,AB是⊙O的直径,⊙O交AC于点D,过点D的直线交BC于点E,交AB的延长线于点P,∠A=∠PDB.
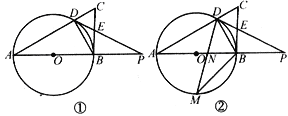
(1)求证:PD是⊙O的切线;
(2)若AB=4,DA=DP,试求弧BD的长;
(3)如图②,点M是弧AB的中点,连结DM,交AB于点N.若tanA=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )
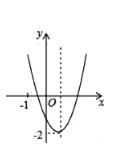
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年清明节前后某茶叶销售商在青山茶厂先后购进两批茶叶.第一批茶叶进货用了5.4万元,进货单价为a元/千克.购回后该销售商将茶叶分类包装出售,把其中300千克精装品以进货单件的两倍出售;余下的简装品以150元/千克的价格出售,全部卖出.第二批进货用了5万元,这一次的进货单价每千克比第一批少了20元.购回分类包装后精装品占总质量的一半,以200元/千克的单价出售;余下的简装品在这批进货单价的基础上每千克加价40元后全部卖出.若其它成本不计,第二批茶叶获得的毛利润是3.5万元.
(1)用含a的代数式表示第一批茶叶的毛利润;
(2)求第一批茶叶中精装品每千克售价.(总售价-总进价=毛利润)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com