
分析 由点C、点D在直线y=kx+b上,可以得出n与m的关系以及q与p的关系,结合“m+p=2,n+q=b2+4b+2”可得出2k=b2+2b+2=(b+1)2+1≥1,由k>0即可得知y=kx+b为增函数,结合m<p即可得出结论.
解答 解:n<q,理由如下:
∵点C(m,n),点D(p,q)在直线y=kx+b,
∴有$\left\{\begin{array}{l}{n=km+b}\\{q=kp+b}\end{array}\right.$,
∴n+q=k(m+p)+2b,
又∵m+p=2,n+q=b2+4b+2,
∴2k+2b=b2+4b+2,即2k=b2+2b+2=(b+1)2+1≥1,
∴k>0,即y=kx+b为增函数.
∵m<p,
∴n<q.
点评 本题考查了一次函数图象上点的坐标特征,解题的关键是找出一次函数一次项系数k>0.本题属于基础题,难度不大,解决该题型题目时,由点在直线上找出点的横纵坐标之间的关系,结合给定的条件想办法找出一次函数一次项系数的正负值是关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| d | 50 | 80 | 100 | 150 |
| h | 25 | 40 | 50 | 75 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
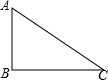 如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )
如图,△ABC中,∠C=30°,∠B=90°,AC=8,以点A为圆心,半径为4的圆与BC的位置关系是( )| A. | 相交 | B. | 相离 | C. | 相切 | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )| A. | 2 | B. | 2$\sqrt{6}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{x+2}$ | B. | 1-x | C. | 1 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com