Question

6．如图1，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D，E分别在边BC，AC上．
（1）当BD=AE=2时，直接写出$\frac{OE}{OB}$=$\frac{7}{8}$，$\frac{OA}{OD}$=$\frac{3}{2}$；
（2）如图2，若O为AD的中点，求证：$\frac{AE}{CE}$=$\frac{BD}{BC}$；
（3）如图3，当$\frac{BD}{AE}$=$\frac{3}{5}$，∠AOE=∠BAC时，求AE的值．

Answer 1

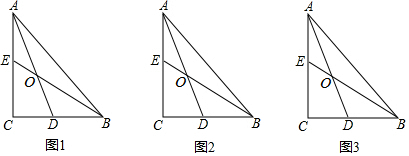
分析 （1）如图1中，作AF∥BC交BE的延长线于F．利用平行线分线段成比例定理，一一求解即可．
（2）如图2中，作DF∥AC交BF于F．利用平行线分线段成比例定理即可解决问题．
（3）如图3中，作EF⊥AB于F．设AE=5k，BD=3k．只要证明△ACD∽△BFE，可得$\frac{AC}{BF}$=$\frac{CD}{EF}$，可得$\frac{4}{5-4k}$=$\frac{3-3k}{3k}$，解方程即可解决问题．

解答 （1）解：如图1中，作AF∥BC交BE的延长线于F．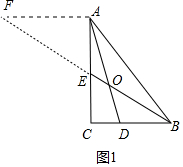

∵AF∥BC，
∴$\frac{AF}{BC}$=$\frac{AE}{EC}$=$\frac{EF}{BE}$，
∵AE=2，AC=4，
∴AE=EC，AF=BC=3，EF=BE，设EF=EB=b，
∵AF∥DB，
∴$\frac{AO}{OD}$=$\frac{AF}{DB}$=$\frac{OF}{OB}$=$\frac{3}{2}$，
∴OF=$\frac{12}{5}$b，OB=$\frac{8}{5}$b，
∴OE=OF-EF=$\frac{7}{5}$b，
∴$\frac{OE}{OB}$=$\frac{\frac{7}{5}b}{\frac{8}{5}b}$=$\frac{7}{8}$，
故答案为$\frac{7}{8}$，$\frac{3}{2}$．

（2）证明：如图2中，作DF∥AC交BF于F．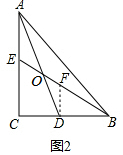

∵DF∥AE，OA=OD，
∴$\frac{OA}{OD}$=$\frac{AE}{DF}$=1
∴AE=DF，
∵DF∥EC，
∴$\frac{DF}{EC}$=$\frac{BD}{BC}$，
∴$\frac{AE}{EC}$=$\frac{BD}{BC}$．

（3）解：如图3中，作EF⊥AB于F．设AE=5k，BD=3k．

∵∠ACB=90°，AC=4，BC=3，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∵∠EAF=∠CAB，∠AFE=∠C=90°，
∴△AEF∽△ABC，
∴$\frac{AE}{AB}$=$\frac{AF}{AC}$=$\frac{EF}{CB}$，
∴AF=4k，EF=3k，
∵∠AOE=∠ACB，
∴∠OAB+∠OBA=∠CAD+∠OAB，
∴∠CAD=∠ABO，∵∠C=∠EFB=90°，
∴△ACD∽△BFE，
∴$\frac{AC}{BF}$=$\frac{CD}{EF}$，
∴$\frac{4}{5-4k}$=$\frac{3-3k}{3k}$，
整理得4k²-13k+5=0，
解得k=$\frac{13-\sqrt{89}}{8}$或$\frac{13+\sqrt{89}}{8}$（舍弃），
∴AE=5k=$\frac{65-\sqrt{89}}{8}$．

点评 本题考查相似三角形的综合题、平行线分线段成比例定理、相似三角形的判定和性质、一元二次方程等知识，解题的关键是学会添加常用辅助线，利用平行线分线段成比例定理解决问题，学会用方程的思考思考问题，属于中考压轴题．