【题目】如图，∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13.求四边形ABCD的面积．
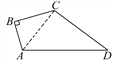
【答案】36.
【解析】试题分析：连接AC，在直角三角形ABC中，由AB及BC的长，利用勾股定理求出AC的长，再由AD及CD的长，利用勾股定理的逆定理得到三角形ACD为直角三角形，根据四边形ABCD的面积=直角三角形ABC的面积+直角三角形ACD的面积，即可求出四边形的面积．
试题解析：解：连接AC．如图所示：
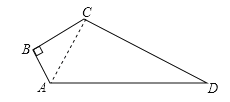
∵∠B=90°，∴△ABC为直角三角形．又∵AB=3，BC=4，∴根据勾股定理得：AC=
=5．又∵CD=12，AD=13，∴AD2=132=169，CD2+AC2=122+52=144+25=169，∴CD2+AC2=AD2，∴△ACD为直角三角形，∠ACD=90°，则S四边形ABCD=S△ABC+S△ACD=
ABBC+ACCD=×3×4+×5×12=36．
故四边形ABCD的面积是36．
科目：初中数学 来源： 题型：
【题目】儿童节期间，某公园游戏场举行一场活动．有一种游戏的规则是：在一个装有8个红球和若干白球(每个球除颜色外，其他都相同)的袋中，随机摸一个球，摸到一个红球就得到一个海宝玩具．已知参加这种游戏的儿童有40 000人，公园游戏场发放海宝玩具8 000个．
(1)求参加此次活动得到海宝玩具的频率？
(2)请你估计袋中白球的数量接近多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
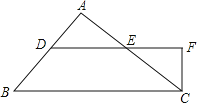
【题目】已知：如图，在△ABC中，∠A＝90°，点D、E分别在AB、AC上，DE∥BC，CF与DE的延长线垂直，垂足为F．
（1)求证：∠B＝∠ECF ；
（2）若∠B＝55°，求∠CED的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1个单位长度的小正方形组成的网格中．
（1）把
平移至
的位置，使点
与
对应，得到
；
（2）图中可用字母表示，与线段
平行且相等的线段有哪些？
（3）求四边形
的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】己知长方形
，
为坐标原点，
点坐标为
，
点在
轴的正半轴上，
点在
轴的正半轴上，
是线段
上的动点，设
，已知点
在第一象限且是直线
上一点，若
是等腰直角三角形．
（
）求点的坐标并写出解题过程．
（
）直角向下平移
个单位后，在该直线上是否存在点，使是等腰直角三角形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了深化改革，某校积极开展校本课程建设，计划成立“文学鉴赏”“科学实验”“音乐舞蹈”和“手工编织”等多个社团，要求每位学生都自主选择其中一个社团．为此，随机调查了本校各年级部分学生选择社团的意向，并将调查结果绘制成如下统计图表(不完整)：
某校被调查学生选择社团意向统计表
选择意向 | 文学鉴赏 | 科学实验 | 音乐舞蹈 | 手工编织 | 其他 |
所占百分比 | a | 35% | b | 10% | c |
根据统计图表中的信息，解答下列问题：
(1)求本次调查的学生总人数及a，b，c的值；
(2)将条形统计图补充完整．
查看答案和解析>>
科目：初中数学 来源： 题型：
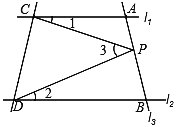
【题目】如图，已知直线l1∥l2，且l3和l1、l2分别交于A、B两点，点P在直线AB上.
（1）试说明∠1，∠2，∠3之间的关系式；（要求写出推理过程）
（2）如果点P在A、B两点之间（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系是否发生变化？（只回答）
（3）如果点P在A、B两点外侧（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系.（要求写出推理过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠ABC=50°，∠ACB=60°，点E在BC的延长线上，∠ABC的平分线BD与∠ACE的平分线CD相交于点D，连接AD，下列结论中不正确的是（ ）
A. ∠BAC=70° B. ∠DOC=90° C. ∠BDC=35° D. ∠DAC=55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
