练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．a=5+2$\sqrt{6}$，b=$\frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{3}-\sqrt{2}}}$，则a与b的关系是（　　）
    A．a=bB．ab=1C．a＞bD．a＜b．

    分析 首先将b分母有理化，再与a比较．

    解答 解：b=$\frac{{\sqrt{3}+\sqrt{2}}}{{\sqrt{3}-\sqrt{2}}}$=$\frac{（\sqrt{3}+\sqrt{2}）（\sqrt{3}+\sqrt{2}）}{（\sqrt{3}-\sqrt{2}）（\sqrt{3}+\sqrt{2}）}$=5$+2\sqrt{6}$，
    ∵a=5$+2\sqrt{6}$，
    ∴a=b，
    故选A．

    点评 本题主要考查了分母有理化，先化简b再比较是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．下列调查中，适合普查的是（　　）
    A．了解某文稿的错别字情况B．了解某种灯泡的使用寿命情况
    C．了解某市学生的视力情况D．了解某市老年人参加晨练的情况．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    3．关于x的方程a（x+m）2+b=0的解是x1=-5，x2=3（a、b、m均为常数，a≠0），则方程a（x+m-2）2+b=0的解是-3，5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．（1）计算：|$\sqrt{3}$-3|+（π-1）0-（-$\frac{1}{2}$）-2+$\root{3}{8}$   
    （2）$\frac{1}{2}$（x-2）2=8，求x．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．已知am=6，an=3，则am+n=18，am-n=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．△ABC与△A′B′C′中，条件①AB=A′B′，②BC=B′C′，③AC=A′C′，④∠A=∠A′，⑤∠B=∠B′，⑥∠C=∠C′，则下列各组条件中不能保证△ABC≌△A′B′C′的是（　　）
    A．①②③B．①③⑤C．①②⑤D．②⑤⑥

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图1，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．
    （1）说明△ADC≌△CEB；
    （2）说明AD+BE=DE；
    （3）当直线MN绕点C旋转到图2的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以说明．

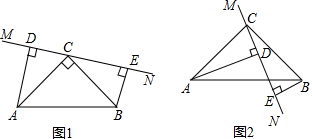
    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

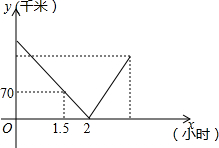    1．一辆中巴车和一辆大巴车分别从甲、乙两站出发，匀速相向而行，相遇后继续前行，已知两车相遇时中巴比大巴多行驶40千米，设行驶的时间为x（小时），两车之间的距离为y（千米），图中的折线表示从两车出发至中巴到达乙站这一过程中y与x之间的函数关系．根据图象提供的信息，可知：当中巴到达乙站时，大巴离甲站的距离为70千米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

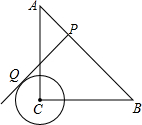    2．如图，等腰Rt△ABC中，∠ACB=90°，AC=BC=4，⊙C的半径为1，点P在斜边AB上，PQ切⊙O于点Q，则切线长PQ长度的最小值为（　　）
    A．$\sqrt{7}$B．2$\sqrt{2}$C．3D．4

    查看答案和解析>>

    同步练习册答案