
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| w |
| 1 |
| x |
| 1 |
| y |
| 1 |
| z |
| 1 |
| w |
| 1 |
| x |
| 1 |
| y |
| 1 |
| y |
| 1 |
| x |
| x-y |
| xy |
| 1 |
| z |
| 1 |
| y |
| y-z |
| yz |
| z-w |
| zw |
| w-x |
| wx |
| x-y |
| xy |
| y-z |
| yz |
| z-w |
| zw |
| w-x |
| wx |
| (x-y)(y-z)(z-w)(w-x) |
| w2x2y2z2 |
| (x-y)(y-z)(z-w)(w-x) |
| w2x2y2z2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
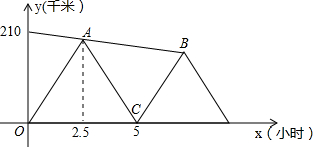 步行速度均近似为匀速,队员上、下车的时间忽略不计).
步行速度均近似为匀速,队员上、下车的时间忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:
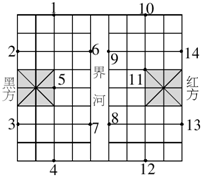 如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?
如图,这是一个中国象棋盘,图中小方格都是相同的正方形(“界河”的宽等于小正方形的边长),假设黑方只有一个“象”,它只能在1,2,3,4,5,6,7位置中的一个,红方有两个“相”,它们只能在8,9,10,11,12,13,14中的两个位置,问:这三个棋子(一个“象”和两个“相”)各在什么位置时,以这三个棋子为顶点构成的三角形的面积最大?查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、21 | B、24 | C、25 | D、37 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com