
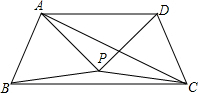
 如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号).
如图,△APB和△DPC是两个全等的等边三角形,AP⊥DP,有以下四个结论:①∠PBC=15°;②AC=BC;③AD∥BC;④直线PC⊥AB,其中正确的结论有①②③④(填序号). 分析 由条件可求得∠BPC=150°,利用等腰三角形的性质可求得∠PBC的度数,可判断①;由条件可证明△APC≌△BPC,可判断②;可分别求得∠DAB=105°,∠ABC=75°,利用平行线的判定可判断③;利用等腰三角形的性质可知PC为AB的垂直平分线,可判断④.
解答 解:
∵△APB和△DPC是两个全等的等边三角形,AP⊥DP,
∴∠APB=∠DPC=60°,∠APD=90°,
∴∠BPC=360°-90°-60°-60°=150°,
∵PB=PC,
∴∠PBC=∠PCB=$\frac{1}{2}$×(180°-150°)=15°,故①正确;
由条件可得∠APC=90°+60°=150°,
∴∠APC=∠BPC,
在△APC和△BPC中
$\left\{\begin{array}{l}{PA=PB}\\{∠APC=∠BPC}\\{PC=PC}\end{array}\right.$
∴△APC≌△BPC(SAS),
∴AC=BC,故②正确;
∵PA=PD,∠APD=90°,
∴∠PAD=45°,
∴∠DAB=45°+60°=105°,
∵∠PBA=60°,∠PBC=15°,
∴∠ABC=75°,
∴∠DAB+∠ABC=180°,
∴AD∥BC,故③正确;
∵△APC≌△BPC,
∴∠ACP=∠BCP,且AC=BC,
∴PC⊥AB,故④正确;
综上可知正确的结论为①②③④,
故答案为:①②③④.
点评 本题主要考查等边三角形的性质、等腰三角形的判定和性质,充分利用图形中角度之间的关系是解题的关键.


科目:初中数学 来源: 题型:选择题
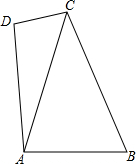 如图,在△ABC中,AC=BC=4,将线段AB绕点A逆时针旋转90°,连接CD,则线段CD的最小值是( )
如图,在△ABC中,AC=BC=4,将线段AB绕点A逆时针旋转90°,连接CD,则线段CD的最小值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$-2 | D. | 4$\sqrt{2}$-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
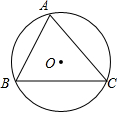 如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°
如图,半径为$\sqrt{2}$的⊙O内接△ABC,∠B=60°,∠C=45°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
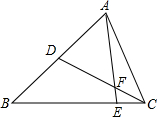 如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30.
如图,在△ABC中,D是AB的中点,E是BC上的一点,且BE=4EC,CD与AE相交于点F.若△CEF的面积为1,则△ABC的面积为30.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com