
【题目】如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)探究:线段OE与OF的数量关系并加以证明;
(2)当点O运动到何处时,且△ABC满足什么条件时,四边形AECF是正方形?
(3)当点O在边AC上运动时,四边形BCFE 是菱形吗?(填“可能”或“不可能”)

【答案】(1)OE=OF.理由见解析;(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由见解析;(3)不可能,理由见解析
【解析】试题分析:(1)由直线MN∥BC,MN交∠BCA的平分线于点E,∠BCA的外角平分线与点F,易证得△OEC与△OFC是等腰三角形,则可证得OE=OF=OC;
(2)这是正方形的判定问题,四边形AECF若是正方形,则必有对角线OA=OC,所以O为AC的中点,同样在△ABC中,当∠ACB=90°时,可满足其为正方形;
(3)此问题是菱形的判定问题,若是菱形,则必有四条边相等,对角线互相垂直.
试题解析:(1)OE=OF.理由如下:
∵CE是∠ACB的角平分线,
∴∠ACE=∠BCE,
又∵MN∥BC,
∴∠NEC=∠ECB,
∴∠NEC=∠ACE,
∴OE=OC,
∵OF是∠BCA的外角平分线,
∴∠OCF=∠FCD,
又∵MN∥BC,
∴∠OFC=∠ECD,
∴∠OFC=∠COF,
∴OF=OC,
∴OE=OF;
(2)当点O运动到AC的中点,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.理由如下:
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形;
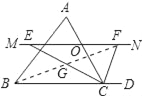
(3)不可能.理由如下:
如图,∵CE平分∠ACB,CF平分∠ACD,
∴∠ECF=![]() ∠ACB+
∠ACB+![]() ∠ACD=
∠ACD=![]() (∠ACB+∠ACD)=90°,
(∠ACB+∠ACD)=90°,
若四边形BCFE是菱形,则BF⊥EC,
但在△GFC中,不可能存在两个角为90°,所以不存在其为菱形.
故答案为不可能.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(–1,2),与x轴的一个交点A在点(–3,0)和(–2,0)之间,其部分图象如下图,则以下结论:①b2–4ac<0;②a+b+c<0;③c–a=2;④方程ax2+bx+c–2=0有两个相等的实数根.其中正确结论的个数为( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 经过
经过![]() 顶点
顶点![]() 的一条直线,
的一条直线,![]() .
.![]() 分别是直线
分别是直线![]() 上两点,且
上两点,且![]() .
.
(1)若直线![]() 经过
经过![]() 的内部,且
的内部,且![]() 在射线
在射线![]() 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若![]() ,
,![]() ,
,
则![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如图2,若![]() ,请添加一个关于
,请添加一个关于![]() 与
与![]() 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线![]() 经过
经过![]() 的外部,
的外部,![]() ,请提出
,请提出![]() 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)请你数一数,图中有______个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.
(1)求证:AC=CD;
(2)若AC=AE,求∠DEC的度数.
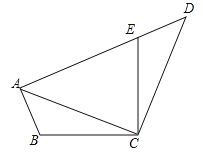
【答案】(1)证明见解析;(2)112.5°.
【解析】试题分析: ![]() 根据同角的余角相等可得到
根据同角的余角相等可得到![]() 结合条件
结合条件![]() ,再加上
,再加上![]() 可证得结论;
可证得结论;![]() 根据
根据![]() 得到
得到![]() 根据等腰三角形的性质得到
根据等腰三角形的性质得到![]() 由平角的定义得到
由平角的定义得到![]()
试题解析: ![]() 证明:
证明:
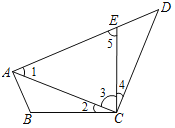
![]()
![]()
![]()
在△ABC和△DEC中,  ,
,
![]()
![]()
(2)∵∠ACD=90°,AC=CD,
∴∠1=∠D=45°,
∵AE=AC,
∴∠3=∠5=67.5°,
∴∠DEC=180°-∠5=112.5°.
【题型】解答题
【结束】
21
【题目】一个零件的形状如图所示,工人师傅按规定做得∠B=90°,
AB=3,BC=4,CD=12,AD=13,假如这是一块钢板,你能帮工人师傅计算一下这块钢板的面积吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在数轴上A、B两点对应的数分别是6,-6,∠DCE=90°(C与O重合,D点在数轴的正半轴上)

(1)如图1,若CF平分∠ACE,则∠AOF=_______;
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.
①当t=1时,α=_________;
②猜想∠BCE和α的数量关系,并证明;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴正半轴向右平移t(0<t<3)个单位,再绕顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0<t<3)个单位,再绕顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α,β满足|α-β|=45°,请用t的式子表示α、β并直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填在相应的大括号内:
﹣5,|-![]() |,﹣12,0,﹣3.14,+1.99,﹣(﹣6),
|,﹣12,0,﹣3.14,+1.99,﹣(﹣6),![]()
(1)正数集合:{ …}
(2)负数集合:{ …}
(3)整数集合:{ …}
(4)分数集合:{ …}.
查看答案和解析>>
科目:初中数学 来源: 题型:
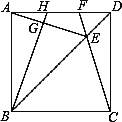
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=BC.连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:
①AH=DF; ②∠AEF=45°; ③S四边形EFHG=S△DEF+S△AGH,
其中正确的结论有_____________________.(填正确的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com