
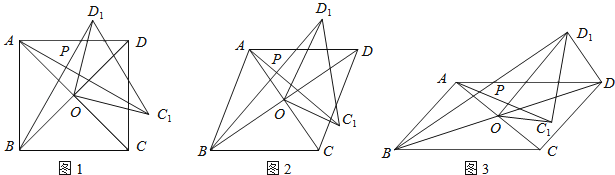
°ĺŐ‚ńŅ°Ņ‘ŕňńĪŖ–őABCD÷–£¨∂‘Ĺ«ŌŖAC°ĘBDŌŗĹĽ”ŕĶ„O£¨Ĺę°ųCOD»∆Ķ„Oįīńś Ī’Ž∑ĹŌÚ–ż◊™Ķ√ĶĹ°ųC1OD1£¨–ż◊™Ĺ«ő™¶»£®0°„£ľ¶»£ľ90°„£©£¨Ń¨Ĺ”AC1°ĘBD1£¨AC1”ŽBD1ĹĽ”ŕĶ„P£ģ
£®1£©»ÁÕľ1£¨»ŰňńĪŖ–őABCD «’ż∑Ĺ–ő£ģ
ĘŔ«ů÷§£ļ°ųAOC1°’°ųBOD1£ģ
Ęŕ«Ž÷ĪĹ”–ī≥ŲAC1 ”ŽBD1ĶńőĽ÷√ĻōŌĶ£ģ
£®2£©»ÁÕľ2£¨»ŰňńĪŖ–őABCD «Ń‚–ő£¨AC£Ĺ5£¨BD£Ĺ7£¨…ŤAC1£ĹkBD1£ģŇ–∂ŌAC1”ŽBD1ĶńőĽ÷√ĻōŌĶ£¨ňĶ√ųņŪ”…£¨≤Ę«ů≥ŲkĶń÷Ķ£ģ
£®3£©»ÁÕľ3£¨»ŰňńĪŖ–őABCD «∆Ĺ––ňńĪŖ–ő£¨AC£Ĺ5£¨BD£Ĺ10£¨Ń¨Ĺ”DD1£¨…ŤAC1£ĹkBD1£ģ«Ž÷ĪĹ”–ī≥ŲkĶń÷ĶļÕAC12+£®kDD1£©2Ķń÷Ķ£ģ
°ĺīūįł°Ņ£®1£©ĘŔŌÍľŻĹ‚őŲ£ĽĘŕAC1°ÕBD1£Ľ£®2£©AC1°ÕBD1£¨ņŪ”…ŌÍľŻĹ‚őŲ£¨k£Ĺ![]() £Ľ£®3£©k£Ĺ
£Ľ£®3£©k£Ĺ![]() £¨ AC12+£®kDD1£©2£Ĺ25£ģ
£¨ AC12+£®kDD1£©2£Ĺ25£ģ
°ĺĹ‚őŲ°Ņ
£®1£©ĘŔ»ÁÕľ1£¨łýĺ›’ż∑Ĺ–őĶń–‘÷ Ķ√OC£ĹOA£ĹOD£ĹOB£¨AC°ÕBD£¨‘Ú°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨‘Ŕłýĺ›–ż◊™Ķń–‘÷ Ķ√OC1£ĹOC£¨OD1£ĹOD£¨°ŌCOC1£Ĺ°ŌDOD1£¨‘ÚOC1£ĹOD1£¨ņŻ”√Ķ»Ĺ«Ķń≤ĻĹ«ŌŗĶ»Ķ√°ŌAOC1£Ĺ°ŌBOD1£¨»Ľļůłýĺ›°įSAS°ĪŅ…÷§√ų°ųAOC1°’°ųBOD1£Ľ
Ęŕ”…°ŌAOB£Ĺ90°„£¨‘Ú°ŌOAB+°ŌABP+°ŌOBD1£Ĺ90°„£¨ňý“‘°ŌOAB+°ŌABP+°ŌOAC1£Ĺ90°„£¨‘Ú°ŌAPB£Ĺ90°„ňý“‘AC1°ÕBD1£Ľ
£®2£©»ÁÕľ2£¨łýĺ›Ń‚–őĶń–‘÷ Ķ√OC£ĹOA£Ĺ![]() AC£¨OD£ĹOB£Ĺ
AC£¨OD£ĹOB£Ĺ![]() BD£¨AC°ÕBD£¨‘Ú°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨‘Ŕłýĺ›–ż◊™Ķń–‘÷ Ķ√OC1£ĹOC£¨OD1£ĹOD£¨°ŌCOC1£Ĺ°ŌDOD1£¨‘ÚOC1£ĹOA£¨OD1£ĹOB£¨ņŻ”√Ķ»Ĺ«Ķń≤ĻĹ«ŌŗĶ»Ķ√°ŌAOC1£Ĺ°ŌBOD1£¨ľ”…Ō
BD£¨AC°ÕBD£¨‘Ú°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨‘Ŕłýĺ›–ż◊™Ķń–‘÷ Ķ√OC1£ĹOC£¨OD1£ĹOD£¨°ŌCOC1£Ĺ°ŌDOD1£¨‘ÚOC1£ĹOA£¨OD1£ĹOB£¨ņŻ”√Ķ»Ĺ«Ķń≤ĻĹ«ŌŗĶ»Ķ√°ŌAOC1£Ĺ°ŌBOD1£¨ľ”…Ō![]() £¨łýĺ›Ōŗň∆»żĹ«–őĶńŇ–∂®∑Ĺ∑®Ķ√ĶĹ°ųAOC1°◊°ųBOD1£¨Ķ√ĶĹ°ŌOAC1£Ĺ°ŌOBD1£¨”…°ŌAOB£Ĺ90°„Ķ√°ŌOAB+°ŌABP+°ŌOBD1£Ĺ90°„£¨‘Ú°ŌOAB+°ŌABP+°ŌOAC1£Ĺ90°„£¨‘Ú°ŌAPB£Ĺ90°„£¨ňý“‘AC1°ÕBD1£Ľ»Ľļůłýĺ›Ōŗň∆Ī»Ķ√ĶĹ
£¨łýĺ›Ōŗň∆»żĹ«–őĶńŇ–∂®∑Ĺ∑®Ķ√ĶĹ°ųAOC1°◊°ųBOD1£¨Ķ√ĶĹ°ŌOAC1£Ĺ°ŌOBD1£¨”…°ŌAOB£Ĺ90°„Ķ√°ŌOAB+°ŌABP+°ŌOBD1£Ĺ90°„£¨‘Ú°ŌOAB+°ŌABP+°ŌOAC1£Ĺ90°„£¨‘Ú°ŌAPB£Ĺ90°„£¨ňý“‘AC1°ÕBD1£Ľ»Ľļůłýĺ›Ōŗň∆Ī»Ķ√ĶĹ £¨ňý“‘k£Ĺ
£¨ňý“‘k£Ĺ![]() £Ľ
£Ľ
£®3£©”Ž£®2£©“Ľ—ýŅ…÷§√ų°ųAOC1°◊°ųBOD1£¨‘Ú![]() £¨ňý“‘k£Ĺ
£¨ňý“‘k£Ĺ![]() £Ľłýĺ›–ż◊™Ķń–‘÷ Ķ√OD1£ĹOD£¨łýĺ›∆Ĺ––ňńĪŖ–őĶń–‘÷ Ķ√OD£ĹOB£¨‘ÚOD1£ĹOB£ĹOD£¨”ŕ «Ņ…Ň–∂Ō°ųBDD1ő™÷ĪĹ«»żĹ«–ő£¨łýĺ›ĻīĻ…∂®ņŪĶ√BD12+DD12£ĹBD2£Ĺ100£¨ňý“‘£®2AC1£©2+DD12£Ĺ100£¨”ŕ «”–AC12+£®kDD1£©2£Ĺ25£ģ
£Ľłýĺ›–ż◊™Ķń–‘÷ Ķ√OD1£ĹOD£¨łýĺ›∆Ĺ––ňńĪŖ–őĶń–‘÷ Ķ√OD£ĹOB£¨‘ÚOD1£ĹOB£ĹOD£¨”ŕ «Ņ…Ň–∂Ō°ųBDD1ő™÷ĪĹ«»żĹ«–ő£¨łýĺ›ĻīĻ…∂®ņŪĶ√BD12+DD12£ĹBD2£Ĺ100£¨ňý“‘£®2AC1£©2+DD12£Ĺ100£¨”ŕ «”–AC12+£®kDD1£©2£Ĺ25£ģ
£®1£©ĘŔ÷§√ų£ļ»ÁÕľ1£¨
°ŖňńĪŖ–őABCD «’ż∑Ĺ–ő£¨
°ŗOC£ĹOA£ĹOD£ĹOB£¨AC°ÕBD£¨
°ŗ°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨
°Ŗ°ųCOD»∆Ķ„Oįīńś Ī’Ž∑ĹŌÚ–ż◊™Ķ√ĶĹ°ųC1OD1£¨
°ŗOC1£ĹOC£¨OD1£ĹOD£¨°ŌCOC1£Ĺ°ŌDOD1£¨
°ŗOC1£ĹOD1£¨°ŌAOC1£Ĺ°ŌBOD1£Ĺ90°„+°ŌAOD1£¨
‘ŕ°ųAOC1ļÕ°ųBOD1÷–
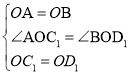 £¨
£¨
°ŗ°ųAOC1°’°ųBOD1£®SAS£©£Ľ
ĘŕAC1°ÕBD1£Ľ
°Ŗ°ŌAOB£Ĺ90°„£¨
°ŗ°ŌOAB+°ŌABP+°ŌOBD1£Ĺ90°„£¨
°ŗ°ŌOAB+°ŌABP+°ŌOAC1£Ĺ90°„£¨‘Ú°ŌAPB£Ĺ90°„
°ŗAC1°ÕBD1£Ľ
£®2£©AC1°ÕBD1£ģ
ņŪ”…»ÁŌ¬£ļ»ÁÕľ2£¨
°ŖňńĪŖ–őABCD «Ń‚–ő£¨
°ŗOC£ĹOA£Ĺ![]() AC£¨OD£ĹOB£Ĺ
AC£¨OD£ĹOB£Ĺ![]() BD£¨AC°ÕBD£¨
BD£¨AC°ÕBD£¨
°ŗ°ŌAOB£Ĺ°ŌCOD£Ĺ90°„£¨
°Ŗ°ųCOD»∆Ķ„Oįīńś Ī’Ž∑ĹŌÚ–ż◊™Ķ√ĶĹ°ųC1OD1£¨
°ŗOC1£ĹOC£¨OD1£ĹOD£¨°ŌCOC1£Ĺ°ŌDOD1£¨
°ŗOC1£ĹOA£¨OD1£ĹOB£¨°ŌAOC1£Ĺ°ŌBOD1£¨
°ŗ![]() £¨
£¨
°ŗ°ųAOC1°◊°ųBOD1£¨
°ŗ°ŌOAC1£Ĺ°ŌOBD1£¨
”÷°Ŗ°ŌAOB£Ĺ90°„£¨
°ŗ°ŌOAB+°ŌABP+°ŌOBD1£Ĺ90°„£¨
°ŗ°ŌOAB+°ŌABP+°ŌOAC1£Ĺ90°„£¨
°ŗ°ŌAPB£Ĺ90°„
°ŗAC1°ÕBD1£Ľ
°Ŗ°ųAOC1°◊°ųBOD1£¨
°ŗ 
°ŗk£Ĺ![]() £Ľ
£Ľ
£®3£©»ÁÕľ3£¨”Ž£®2£©“Ľ—ýŅ…÷§√ų°ųAOC1°◊°ųBOD1£¨
°ŗ![]() £¨
£¨
°ŗk£Ĺ![]() £Ľ
£Ľ
°Ŗ°ųCOD»∆Ķ„Oįīńś Ī’Ž∑ĹŌÚ–ż◊™Ķ√ĶĹ°ųC1OD1£¨
°ŗOD1£ĹOD£¨
∂ÝOD£ĹOB£¨
°ŗOD1£ĹOB£ĹOD£¨
°ŗ°ųBDD1ő™÷ĪĹ«»żĹ«–ő£¨
‘ŕRt°ųBDD1÷–£¨
BD12+DD12£ĹBD2£Ĺ100£¨
°ŗ£®2AC1£©2+DD12£Ĺ100£¨
°ŗAC12+£®kDD1£©2£Ĺ25£ģ




 Ķŕ1ĺŪĶ•‘™‘¬Ņľ∆ŕ÷–∆ŕń©ŌĶŃ–īūįł
Ķŕ1ĺŪĶ•‘™‘¬Ņľ∆ŕ÷–∆ŕń©ŌĶŃ–īūįł
| ńÍľ∂ | łŖ÷–Ņő≥Ő | ńÍľ∂ | ≥ű÷–Ņő≥Ő |
| łŖ“Ľ | łŖ“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű“Ľ | ≥ű“Ľ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ∂Ģ | łŖ∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű∂Ģ | ≥ű∂Ģ√‚∑—Ņő≥ŐÕ∆ľŲ£° |
| łŖ»ż | łŖ»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° | ≥ű»ż | ≥ű»ż√‚∑—Ņő≥ŐÕ∆ľŲ£° |
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
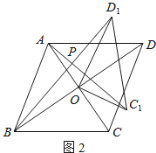
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨![]() «
«![]() ĶńŌ“£¨
ĶńŌ“£¨![]() ĹĽ
ĹĽ![]() ”ŕĶ„
”ŕĶ„![]() £¨ĻżĶ„
£¨ĻżĶ„![]() Ķń÷ĪŌŖĹĽ
Ķń÷ĪŌŖĹĽ![]() Ķń—”≥§ŌŖ”ŕĶ„
Ķń—”≥§ŌŖ”ŕĶ„![]() £ģ«“
£ģ«“![]() £ģ
£ģ
(1)«ů÷§£ļ![]() «
«![]() Ķń«–ŌŖ£ģ
Ķń«–ŌŖ£ģ
(2)»Ű![]() ĶńįŽĺ∂ő™
ĶńįŽĺ∂ő™![]() £¨
£¨![]() £¨‘Ú
£¨‘Ú![]() Ķń≥§ő™ £ģ
Ķń≥§ő™ £ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
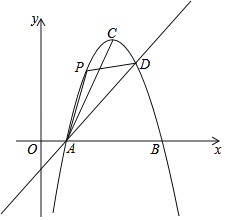
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨÷ĪŌŖy£Ĺx©Ā1”ŽŇ◊őÔŌŖy£Ĺ©Āx2+6x©Ā5ŌŗĹĽ”ŕA°ĘDŃĹĶ„£ģŇ◊őÔŌŖĶń∂•Ķ„ő™C£¨Ń¨ĹŠAC£ģ
£®1£©«ůA£¨DŃĹĶ„Ķń◊ÝĪÍ£Ľ
£®2£©Ķ„Pő™ł√Ň◊őÔŌŖ…Ō“Ľ∂ĮĶ„£®”ŽĶ„A°ĘD≤Ľ÷ōļŌ£©£¨Ń¨Ĺ”PA°ĘPD£ģ
ĘŔĶĪĶ„PĶńļŠ◊ÝĪÍő™2 Ī£¨«ů°ųPADĶń√śĽż£Ľ
ĘŕĶĪ°ŌPDA£Ĺ°ŌCAD Ī£¨÷ĪĹ”–ī≥ŲĶ„PĶń◊ÝĪÍ£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨∂‘’Řĺō–ő÷Ĺ∆¨ABCD£¨ ĻAD”ŽBC÷ōļŌ£¨Ķ√ĶĹ’ŘļŘEF£¨į—÷Ĺ∆¨’Ļ∆Ĺ£¨‘Ŕ“Ľīő’ŘĶĢ÷Ĺ∆¨£¨ ĻĶ„A¬š‘ŕEF…ŌĶńĶ„A°šī¶£¨≤Ę Ļ’ŘļŘĺ≠ĻżĶ„B£¨Ķ√ĶĹ’ŘļŘBM£¨»Űĺō–ő÷Ĺ∆¨ĶńŅŪAB=4£¨‘Ú’ŘļŘBMĶń≥§ő™( )
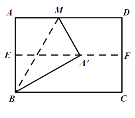
A.![]() B.
B.![]() C.8D.
C.8D.![]()
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ»ÁÕľ£¨‘ŕ∆Ĺ√ś÷ĪĹ«◊ÝĪÍŌĶ÷–£¨Ń‚–őABCD‘ŕĶŕ“ĽŌůŌřńŕ£¨ĪŖBC”Žx÷Š∆Ĺ––£¨A£¨BŃĹĶ„Ķń◊›◊ÝĪÍ∑÷Īūő™4£¨2£¨∑īĪ»ņżļĮ ży![]() £®x£ĺ0£©ĶńÕľŌůĺ≠ĻżA£¨BŃĹĶ„£¨»ŰŃ‚–őABCDĶń√śĽżő™2
£®x£ĺ0£©ĶńÕľŌůĺ≠ĻżA£¨BŃĹĶ„£¨»ŰŃ‚–őABCDĶń√śĽżő™2![]() £¨‘ÚkĶń÷Ķő™£®°°°°£©
£¨‘ÚkĶń÷Ķő™£®°°°°£©

A. 2B. 3C. 4D. 6
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņő™”≠Ĺ”![]() ńÍ÷–°Ę»’°Ęļ껿Ļķ«ŗ…ŔńÍťŌť≠«ÚĪ»»Ł£¨ńŌ—Ň÷–—ßľ∆Ľģ∂‘√śĽżő™
ńÍ÷–°Ę»’°Ęļ껿Ļķ«ŗ…ŔńÍťŌť≠«ÚĪ»»Ł£¨ńŌ—Ň÷–—ßľ∆Ľģ∂‘√śĽżő™![]() ‘ň∂Į≥°ĹÝ––ň‹Ĺļłń‘ž.ĺ≠Õ∂ĪÍ£¨”…ľ◊°Ę““ŃĹłŲĻ§≥Ő∂”ņīÕÍ≥…£¨“—÷™ľ◊∂”√ŅŐžń‹łń‘žĶń√śĽż «““∂”√ŅŐžń‹łń‘ž√śĽżĶń
‘ň∂Į≥°ĹÝ––ň‹Ĺļłń‘ž.ĺ≠Õ∂ĪÍ£¨”…ľ◊°Ę““ŃĹłŲĻ§≥Ő∂”ņīÕÍ≥…£¨“—÷™ľ◊∂”√ŅŐžń‹łń‘žĶń√śĽż «““∂”√ŅŐžń‹łń‘ž√śĽżĶń![]() Ī∂£¨≤Ę«“‘ŕ∂ņŃĘÕÍ≥…√śĽżő™
Ī∂£¨≤Ę«“‘ŕ∂ņŃĘÕÍ≥…√śĽżő™![]() Ķńłń‘ž Ī£¨ľ◊∂”Ī»““∂”…Ŕ”√
Ķńłń‘ž Ī£¨ľ◊∂”Ī»““∂”…Ŕ”√![]() Őž.
Őž.
£®1£©«ůľ◊°Ę““ŃĹĻ§≥Ő∂”√ŅŐžń‹ÕÍ≥…ň‹Ĺļłń‘žĶń√śĽż£Ľ
£®2£©…Ťľ◊Ļ§≥Ő∂” ©Ļ§![]() Őž£¨““Ļ§≥Ő∂” ©Ļ§
Őž£¨““Ļ§≥Ő∂” ©Ļ§![]() Őž£¨ł’ļ√ÕÍ≥…łń‘ž»őőŮ£¨«ů
Őž£¨ł’ļ√ÕÍ≥…łń‘ž»őőŮ£¨«ů![]() ”Ž
”Ž![]() ĶńļĮ żĹ‚őŲ Ĺ£Ľ
ĶńļĮ żĹ‚őŲ Ĺ£Ľ
£®3£©»Űľ◊∂”√ŅŐžłń‘ž∑—”√ «![]() ÕÚ‘™£¨““∂”√ŅŐžłń‘ž∑—”√ «
ÕÚ‘™£¨““∂”√ŅŐžłń‘ž∑—”√ «![]() ÕÚ‘™£¨«“ľ◊°Ę““ŃĹ∂” ©Ļ§Ķń◊‹Őž ż≤Ľ≥¨Ļż
ÕÚ‘™£¨«“ľ◊°Ę““ŃĹ∂” ©Ļ§Ķń◊‹Őž ż≤Ľ≥¨Ļż![]() Őž£¨»Áļőį≤ŇŇľ◊°Ę““ŃĹ∂” ©Ļ§ĶńŐž ż£¨ Ļ ©Ļ§◊‹∑—”√◊ÓĶÕ£Ņ≤Ę«ů≥Ų◊ÓĶÕĶń∑—”√.
Őž£¨»Áļőį≤ŇŇľ◊°Ę““ŃĹ∂” ©Ļ§ĶńŐž ż£¨ Ļ ©Ļ§◊‹∑—”√◊ÓĶÕ£Ņ≤Ę«ů≥Ų◊ÓĶÕĶń∑—”√.
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
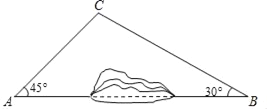
°ĺŐ‚ńŅ°Ņő™ľ”Ņž≥«ŌÁ∂‘Ĺ”£¨Ĺ®…Ť»ę”Ú√ņņŲŌÁīŚ£¨ń≥Ķō«Ý∂‘A°ĘBŃĹĶōľšĶńĻę¬∑ĹÝ––łńĹ®£ģ»ÁÕľ£¨A°ĘBŃĹĶō÷ģľš”–“Ľ◊ý…Ĺ£¨∆Ż≥Ķ‘≠ņīī”AĶōĶĹBĶō–ŤÕĺĺ∂CĶō—ō’ŘŌŖACB–– Ľ£¨Ō÷Ņ™Õ®ňŪĶņļů£¨∆Ż≥ĶŅ…÷ĪĹ”—ō÷ĪŌŖAB–– Ľ£ģ“—÷™BC=80«ß√◊£¨°ŌA=45°„£¨°ŌB=30°„£ģ
£®1£©Ņ™Õ®ňŪĶņ«į£¨∆Ż≥Ķī”AĶōĶĹBĶōīů‘ľ“™◊Ŗ∂ŗ…Ŕ«ß√◊£Ņ
£®2£©Ņ™Õ®ňŪĶņļů£¨∆Ż≥Ķī”AĶōĶĹBĶōīů‘ľŅ…“‘…Ŕ◊Ŗ∂ŗ…Ŕ«ß√◊£Ņ£®ĹŠĻŻĺę»∑ĶĹ0.1«ß√◊£©£®≤őŅľ żĺ›£ļ![]() °÷1.41£¨
°÷1.41£¨![]() °÷1.73£©
°÷1.73£©
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņ£®12∑÷£©»ÁÕľ£¨“—÷™»żĹ«–őABCĶńĪŖAB «°—OĶń«–ŌŖ£¨«–Ķ„ő™B£ģACĺ≠Ļż‘≤–ńO≤Ę”Ž‘≤ŌŗĹĽ”ŕĶ„D°ĘC£¨ĻżC◊ų÷ĪŌŖCEĀAAB£¨ĹĽABĶń—”≥§ŌŖ”ŕĶ„E£ģ
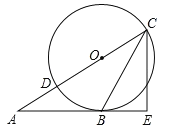
£®1£©«ů÷§£ļCB∆Ĺ∑÷°ŌACE£Ľ
£®2£©»ŰBE=3£¨CE=4£¨«ů°—OĶńįŽĺ∂£ģ
≤ťŅīīūįłļÕĹ‚őŲ>>
Ņ∆ńŅ£ļ≥ű÷– ż—ß ņī‘ī£ļ Ő‚–Õ£ļ
°ĺŐ‚ńŅ°Ņń≥Ļ§“’∆∑≥ß…ķ≤ķ“Ľ÷÷∆Ż≥Ķ◊į ő∆∑£¨√ŅľĢ…ķ≤ķ≥…Īĺő™20‘™£¨Ōķ ؾسّŕ30‘™÷Ń80‘™÷ģľš£®ļ¨30‘™ļÕ80‘™£©£¨Ōķ ŘĻż≥Ő÷–ĶńĻ‹ņŪ°Ę≤÷īĘ°Ę‘ň šĶ»łų÷÷∑—”√£®≤Ľļ¨…ķ≤ķ≥…Īĺ£©◊‹ľ∆50ÕÚ‘™£¨∆šŌķ ŘŃŅy£®ÕÚłŲ£©”ŽŌķ ŘľŘłŮ£®‘™/łŲ£©ĶńļĮ żĻōŌĶ»ÁÕľňý ĺ£ģ
£®1£©ĶĪ30°‹x°‹60 Ī£¨«ůy”ŽxĶńļĮ żĻōŌĶ Ĺ£Ľ
£®2£©«ů≥Ųł√≥ß…ķ≤ķŌķ Ř’‚÷÷≤ķ∆∑ĶńīŅņŻ»ůw£®ÕÚ‘™£©”ŽŌķ ؾسŮx£®‘™/łŲ£©ĶńļĮ żĻōŌĶ Ĺ£Ľ
£®3£©Ōķ ؾسٔ¶∂®ő™∂ŗ…Ŕ‘™ Ī£¨ĽŮĶ√ņŻ»ů◊Óīů£¨◊ÓīůņŻ»ů «∂ŗ…Ŕ£Ņ

≤ťŅīīūįłļÕĹ‚őŲ>>
įŔ∂»÷¬–Ň - Ń∑Ōį≤ŠŃ–ĪŪ - ‘Ő‚Ń–ĪŪ
ļĢĪĪ °Ľ•Ń™ÕÝő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®∆ĹŐ® | ÕÝ…Ō”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | ĶÁ–Ň’©∆≠ĺŔĪ®◊®«Ý | …śņķ ∑–ťőř÷ų“Ś”–ļ¶–ŇŌĘĺŔĪ®◊®«Ý | …ś∆ů«÷»®ĺŔĪ®◊®«Ý
ő•∑®ļÕ≤ĽŃľ–ŇŌĘĺŔĪ®ĶÁĽį£ļ027-86699610 ĺŔĪ®” Ōš£ļ58377363@163.com