
【题目】如图,一次函数的图象与反比例函数的图象交于A(﹣3,1)、B(m,3)两点,
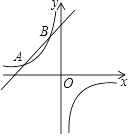
(1)求反比例函数和一次函数的解析式;
(2)写出使一次函数的值大于反比例函数的x的取值范围;
(3)连接AO、BO,求△ABO的面积.
【答案】(1)y=﹣ ![]() ,y=x+4;(2)﹣3<x<﹣1或x>0;(3)4.
,y=x+4;(2)﹣3<x<﹣1或x>0;(3)4.
【解析】
(1) 设一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ,把
,把![]() 代入
代入![]() 即可求出反比例函数的解析式, 把
即可求出反比例函数的解析式, 把![]() 代入
代入![]() 求出
求出![]() 的坐标, 把
的坐标, 把![]() 、
、![]() 的坐标代入
的坐标代入![]() 求出
求出![]() 、
、![]() ,即可求出一次函数的解析式;
,即可求出一次函数的解析式;
(2) 根据![]() 、
、![]() 的坐标和图象得出即可;
的坐标和图象得出即可;
(3) 求出一次函数和两坐标轴的交点坐标, 再根据三角形的面积公式求出即可 .
解: (1) 设一次函数的解析式为![]() ,反比例函数的解析式为
,反比例函数的解析式为![]() ,
,
把![]() 代入
代入![]() 得:
得:![]() ,
,
即反比例函数的解析式为![]() ,
,
把![]() 代入
代入![]() 得:
得:![]() ,
,
解得:![]() ,
,
即![]() 的坐标为
的坐标为![]() ,
,
把![]() 、
、![]() 的坐标代入
的坐标代入![]() 得:
得:![]() ,
,
解得:![]() ,
,![]() ,
,
即一次函数的解析式为![]() ;
;
(2)![]() 函数
函数![]() 和
和![]() 的交点为
的交点为![]() 、
、![]() ,
,
![]() 使一次函数的值大于反比例函数的
使一次函数的值大于反比例函数的![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
(3)设一次函数![]() 和
和![]() 轴的交点为
轴的交点为![]() ,和
,和![]() 轴的交点为
轴的交点为![]() ,
,

当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
即![]() ,
,![]() ,
,
![]() 、
、![]() ,
,
![]() 的面积为
的面积为![]() .
.


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:![]() (p,q是正整数,且
(p,q是正整数,且![]() ),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:
),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的完美分解.并规定:![]() .
.
例如18可以分解成1×18,2×9或3×6,因为18-1>9-2>6-3,所以3×6是18的完美分解,所以F(18)=![]() .
.
(1)F(13)= ,F(24)= ;
(2)如果一个两位正整数t,其个位数字是a,十位数字为![]() ,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
,交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数为“和谐数”,求所有“和谐数”;
(3)在(2)所得“和谐数”中,求F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一渔船自西向东追赶鱼群,在A处测得某无名小岛C在北偏东60°方向上,前进2nmile到达点B处,此时测得无名小岛C在东北方向上.已知无名小岛周围2.5nmile内有暗礁.问:渔船继续追赶鱼群有无触礁危险?
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售A、B两种不同型号的电风扇,每种型号电风扇的购买单价分别为每台310元,460元.
(1)若某单位购买A,B两种型号的电风扇共50台,且恰好支出20000元,求A,B两种型号电风扇各购买多少台?
(2)若购买A,B两种型号的电风扇共50台,且支出不超过18000元,求A种型号电风扇至少要购买多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
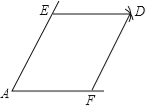
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是⊙O外一点,PA切⊙O于点A,AB是⊙O的直径,连接OP,过点B作BC∥OP交⊙O于点C,连接AC交OP于点D.
(1)求证:PC是⊙O的切线;
(2)若PD=![]() cm,AC=8cm,求图中阴影部分的面积;
cm,AC=8cm,求图中阴影部分的面积;
(3)在(2)的条件下,若点E是弧AB的中点,连接CE,求CE的长.
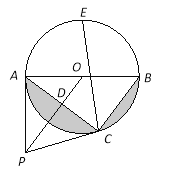
查看答案和解析>>
科目:初中数学 来源: 题型:
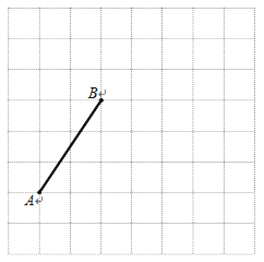
【题目】下图是由边长为1个单位长度的小正方形组成的网格,线段AB的端点在格点上.
(1)请建立适当的平面直角坐标系xOy,使得A点的坐标为(-3,-1),在此坐标系下,B点的坐标为________________;
(2)将线段BA绕点B逆时针旋转90°得线段BC,画出BC;在第(1)题的坐标系下,C点的坐标为__________________;
(3)在第(1)题的坐标系下,二次函数y=ax2+bx+c(a≠0)的图象过O、B、C三点,则此函数图象的对称轴方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根据点
根据点![]() 的坐标建立坐标系,即可写出点
的坐标建立坐标系,即可写出点![]() 的坐标.
的坐标.
![]() 画出点
画出点![]() 旋转后的对应点
旋转后的对应点![]() 连接
连接![]() ,写出点
,写出点![]() 的坐标.
的坐标.
![]() 用待定系数法求出函数解析式,即可求出对称轴方程.
用待定系数法求出函数解析式,即可求出对称轴方程.
详解:(1)建立坐标系如图,
B点的坐标为![]() ;
;
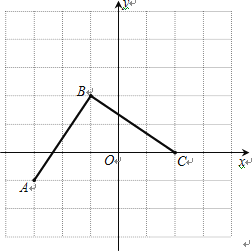
(2)线段BC如图,C点的坐标为![]()
(3)把点![]() 代入二次函数
代入二次函数![]() ,得
,得
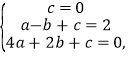
解得: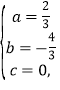
二次函数解析为:![]()
对称轴方程为:![]()
故对称轴方程是![]()
点睛:考查图形与坐标;旋转、对称变换;待定系数法求二次函数解析式,二次函数的图象与性质.熟练掌握各个知识点是解题的关键.
【题型】解答题
【结束】
18
【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C,B+C=10,A>3),那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2021,61×69=4209.
(1)请你直接写出83×87的值;
(2)设这两个两位数的十位数字为x(x>3),个位数字分别为y和z(y+z=10),通过计算验证这两个两位数的乘积为100x(x+1)+yz.
(3)99991×99999=___________________(直接填结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com