
如图,P为△ABC内一点,连接PA、PB、PC,在△PAB、△PBC和△PAC中,如果存在一个三角形与△ABC相似,那么就称P为△ABC的自相似点.
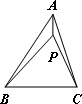
(1)如图,已知Rt△ABC中,∠ACB=90°,∠ACB>∠A,CD是AB上的中线,过点B作BE⊥CD,垂足为E,试说明E是△ABC的自相似点.
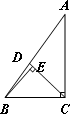
(2)在△ABC中,∠A<∠B<∠C.
①如图,利用尺规作出△ABC的自相似点P(写出作法并保留作图痕迹);
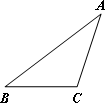
②若△ABC的内心P是该三角形的自相似点,求该三角形三个内角的度数.
|
解:(1)在Rt△ABC中,∠ACB=90°,CD是AB上的中线,∴ ∴∠BCE=∠ABC.∵BE⊥CD,∴∠BEC=90°,∴∠BEC=∠ACB.∴△BCE∽△ABC. ∴E是△ABC的自相似点. (2)①作图略. 作法如下:(i)在∠ABC内,作∠CBD=∠A; (ii)在∠ACB内,作∠BCE=∠ABC;BD交CE于点P. 则P为△ABC的自相似点. ②连接PB、PC.∵P为△ABC的内心,∴ ∵P为△ABC的自相似点,∴△BCP∽△ABC. ∴∠PBC=∠A,∠BCP=∠ABC=2∠PBC=2∠A, ∠ACB=2∠BCP=4∠A.∵∠A+∠ABC+∠ACB=180°. ∴∠A+2∠A+4∠A=180°. ∴ |


科目:初中数学 来源: 题型:
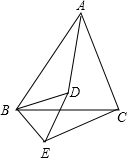 已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、
已知,如图,D为△ABC内一点连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD,BE、| BC |
| AB |
| BE |
| BD |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com