
分析 (1)(3)(5)(6)根据有理数的混合运算的运算方法,求出每个算式的值各是多少即可.
(2)应用加法交换律和加法结合律,求出算式的值是多少即可.
(4)应用乘法分配律,求出算式的值是多少即可.
解答 解:(1)12-(-18)-(+7)-15
=30-7-15
=23-15
=8
(2)$\frac{1}{2}-2\frac{1}{4}-3\frac{1}{2}+2.25$
=($\frac{1}{2}$-3$\frac{1}{2}$)+(2.25-2$\frac{1}{4}$)
=-3+0
=-3
(3)25$-3\frac{1}{2}×(-\frac{6}{7})-(-10)÷(-\frac{2}{3})$
=25+3-15
=28-15
=13
(4)$-1-48×(\frac{5}{24}-\frac{3}{16}+\frac{1}{6})$
=-1-48×$\frac{5}{24}$+48×$\frac{3}{16}$-48×$\frac{1}{6}$
=-1-10+9-8
=-10
(5)$(-\frac{1}{36})÷(-\frac{2}{9}+\frac{1}{3}-\frac{1}{6}+\frac{1}{4})$
=(-$\frac{1}{36}$)÷$\frac{7}{36}$
=-$\frac{1}{7}$
(6)$-{2^2}-[{(-3)×(-\frac{4}{3})-{{(-2)}^3}}]$
=-4-[4-(-8)]
=-4-12
=-16
点评 此题主要考查了有理数的混合运算,要熟练掌握,注意明确有理数混合运算顺序:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先做括号内的运算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.
已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,当其中一点到达终点后,另外一点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
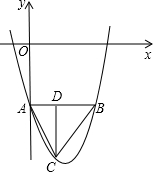 如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).
如图,已知二次函数y=ax2+bx+c的图象的顶点的坐标为(2,-9),与y轴交于点A(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
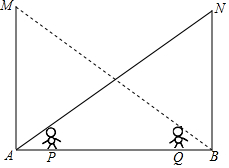 如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.
如图,舞台的左上角和右上角分别吊有灯泡M,N,灯高9.6米,身高均为1.6米的甲、乙两演员分别站在舞台的P,Q处,此时灯M对乙的影子的顶部正好落在灯N的正下方.灯N对甲的影子的顶部也正好落在灯M的正下方,甲、乙两演员相距6米,求舞台AB的宽.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com