
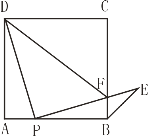
【题目】如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当![]() 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
【答案】(1)证明见解析(2)45°(3)见解析
【解析】
(1)根据∠ADP与∠EPB都是∠APD的余角,根据同角的余角相等,即可求证;
(2)首先证得△PAD≌△EQP,可以证得△BEQ是等腰直角三角形,可以证得∠EBQ=45°,即可证得∠CBE=45°;
(3)这两个三角形是直角三角形,若相似,则对应边的比相等,即可求得![]() 的值.
的值.
(1)证明:∵四边形ABCD是正方形.
∴∠A=∠PBC=90°,AB=AD,
∴∠ADP+∠APD=90°,
∵∠DPE=90°,
∴∠APD+∠EPB=90°,
∴∠ADP=∠EPB;
(2)解:过点E作EQ⊥AB交AB的延长线于点Q,则∠EQP=∠A=90°,

又∵∠ADP=∠EPB,PD=PE,
∴△PAD≌△EQP,
∴EQ=AP,AD=AB=PQ,
∴AP=EQ=BQ,
∴∠CBE=∠EBQ=45°;
(3)![]() .
.
理由:∵△PFD∽△BFP,
∴![]() ,
,
∵∠ADP=∠EPB,∠CBP=∠A
∴△DAP∽△PBF
∴![]() ,
,
∴PA=PB
∴当![]() 时,△PFD∽△BFP.
时,△PFD∽△BFP.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
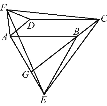
【题目】如图,在平行四边形ABCD中,分别以AB、AD为边向外作等边△ABE、△ADF,延长CB交AE于点G,点G在点A、E之间,连接CE、CF,EF,则以下四个结论一定正确的是:①△CDF≌△EBC;②∠CDF=∠EAF;③△ECF是等边△;④CG⊥AE( )
A. 只有①② B. 只有①②③ C. 只有③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)中,函数 y 与自变量 x 的部分对应值如下表:
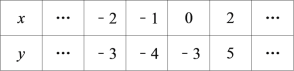
(1)求二次函数的解析式;
(2)求该函数图象与 x 轴的交点坐标;
(3)不等式 ax2+bx+c+3>0 的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
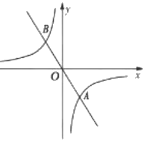
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
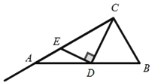
【题目】如图,在ABC中,ACB 90,BAC 30, AB2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当ADE为等腰三角形时,AD的长度为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数学课上,老师提出利用尺规作图完成下面问题:
已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小明的做法如下:
如图
①作线段AB的垂直平分线m;
②作线段BC的垂直平分线n,与直线m交于点O;
③以点O为圆心,OA为半径作△ABC的外接圆;
④在弧ACB上取一点P,连结AP,BP.
所以∠APB=∠ACB.
老师说:“小明的作法正确.”
请回答:
(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为 m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】淘宝网举办“双十一”购物活动许多商家都会利用这个契机进行打折让利的促销活动.
(1)甲网店销售的![]() 商品的成本为30元/件,网上标价为80元/件.“双十一”购物活动当天,甲网店连续两次降价销售
商品的成本为30元/件,网上标价为80元/件.“双十一”购物活动当天,甲网店连续两次降价销售![]() 商品吸引顾客,问该店平均每次降价率为多少时,才能使
商品吸引顾客,问该店平均每次降价率为多少时,才能使![]() 商品的售价为39.2元/件?
商品的售价为39.2元/件?
(2)乙网店销售一批名牌衬衫,平均每天销售20件,每件盈利40元,为了扩大销售,增加盈利减少库存,商场决定采取适当的降价措施,经调查发现,如果每件降价1元,则每天可多售2件.商场若想每天盈利1200元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷每人必选且只选一种,在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:

(1)这次统计共抽查了________名学生;在扇形统计图中,表示“![]() ”的扇形所占百分数为__________;
”的扇形所占百分数为__________;
(2)将条形统计图补充完整;
(3)该校共有![]() 名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“![]() ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com