练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在正五边形ABCDE中，对角线AC、BE交于F点．

    求证：CF2＝CA·AF．

    答案：
    解析：

    作正五边形ABCDE的外接圆⊙O，如图所示．∵五边形ABCDE是正五边形，圆周，即的度数都等于，

    ∴∠BAC＝∠ACB＝∠ABF＝，∴△ABF∽△ACB，∴AF∶AB＝AB∶AC，∴AB2＝CA·AF．在△CBF中，∠BCF＝36°，∠CBF＝72°，∴∠BFC＝180°－∠BCF－∠CBF＝72°，∴CF＝CB，又AB＝CB，∴CF＝AB，∴CF2＝CA·AF．


    提示：

    在解决有关正多边形的问题中，可以利用正多边形与圆的特殊关系，作出正多边形的外接圆或内切圆，再利用正多边形的一些性质，将会得到一些结论，为进一步的证明提供很多条件．因此，作正多边形的外接圆或内切圆是常用到的辅助线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、问题背景：某课外学习小组在一次学习研讨中，得到了如下命题：
    如图①，在正五边形ABCDE中，M、N分别是CD、DE上的点，BM与CN相交于点O，若CM=DN，则∠BON=108°．
    该小组提出了一个大胆的猜想：如图②，在正五边形ABCDE中，M、N分别是DE、EA上的点，BM与CN相交于点O，若DM=EN，则∠BON=108°．
    请问他们的猜想是否正确？若正确，请写出解答过程；若不正确，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    问题背景：某课外学习小组在一次学习研讨中，得到了如下两个命题：
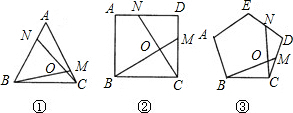
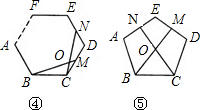
    精英家教网精英家教网
    ①如图1，在正三角形ABC中，M，N分别是AC，AB上的点，BM与CN相交于点O，若∠BON=60°，则BM=CN；
    ②如图2，在正方形ABCD中，M，N分别是CD，AD上的点，BM与CN相交于点O，若∠BON=90°，则BM=CN．
    然后运用类比的思想提出了如下命题；
    ③如图3，在正五边形ABCDE中，M，N分别是CD，DE上的点，BM与CN相交于点O，若∠BON=108°，则BM=CN．任务要求：
    （1）请你从①，②，③三个命题中选择一个进行证明；
    （2）请你继续完成下面的探索：
    ①如图4，在正n（n≥3）边形ABCDEF…中，M，N分别是CD，DE上的点，BM与CN相交于点O，试问当∠BON等于多少度时，结论BM=CN成立；（不要求证明）
    ②如图5，在正五边形ABCDE中，M，N分别是DE，AE上的点，BM与CN相交于点O，若∠BON=108°时，试问结论BM=CN是否还成立．若成立，请给予证明；若不成立，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    知识回顾：
    （1）如图1，在△ABC中，点D、E、F分别是边AB、BC、AC的中点，我们把△DEF称为△ABC的中点三角形．则S△DEF：S△ABC=
     
    ；
    （2）如图2，在正方形ABCD中，点E、F、G、H分别是边AB、BC、CD、DA的中点，我们把四边形EFGH称为正方形ABCD的中点四边形，此时四边形EFGH的形状是
     
    ，S四边形EFGH：S四边形ABCD=
     
    ；
    （3）实践探究：
    如图3，在正五边形ABCDE中，若点F、G、H、M、N分别是边AB、BC、CD、DE、EA的中点，则中点五边形FGHMN的形状是
     
    ；若正五边形ABCDE的中心为点O，连接OE、ON，求S五边形FGHMN：S五边形ABCDE的值．
    精英家教网
    （4）拓展归纳：
    在正n边形A1A2 …An中，若点B1、B2 …Bn分别是边A1A2、A2A3、…、AnA1的中点，则中点n边形B1B2 …Bn的面积与正n边形A1A2 …An的面积之比为Sn边形B1B2…Bn：Sn边形A1A2…An=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    7、如图，在正五边形ABCDE中，对角线AD，AC与EB分别相交于点M，N．下列结论错误的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

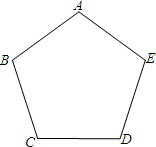    （2013•台湾）如图，甲、乙两人想在正五边形ABCDE内部找一点P，使得四边形ABPE为平行四边形，其作法如下：
    （甲） 连接BD、CE，两线段相交于P点，则P即为所求
    （乙） 先取CD的中点M，再以A为圆心，AB长为半径画弧，交AM于P点，则P即为所求．
    对于甲、乙两人的作法，下列判断何者正确？（　　）

    查看答案和解析>>

    同步练习册答案