
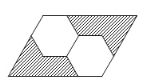
【题目】如图所示,平行四边形内有两个全等的正六边形,若阴影部分的面积记为![]() ,平行四边形的面积记为
,平行四边形的面积记为![]() ,则
,则![]() 的值为____.
的值为____.
【答案】![]()
【解析】
如解图所示:延长EN交BC于点F,过点E作EP⊥BC于P,过点F作FQ⊥MN于Q,过点A作AD⊥BC于D,由图可知,图中两个阴影部分面积相等,证出△BEF为等边三角形,四边形NFGM为菱形,求出等边三角形的边长、菱形的边长和平行四边形的边长,利用锐角三角函数求出等边三角形的高、菱形的高和平行四边形的高,即可求出结论.
解:如下图所示,延长EN交BC于点F,过点E作EP⊥BC于P,过点F作FQ⊥MN于Q,过点A作AD⊥BC于D,
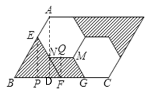
∵平行四边形内有两个全等的正六边形,设正六边形的边长为a
∴∠AEN=∠A=∠ENM=∠MGC=120°,NM∥BC,AE=EN=NM=MG=a
∴∠B=180°-∠A=60°,∠FNM=180°-∠ENM =60°,∠BEF=180°-∠AEN=60°,∠NFG=∠ENM=120°=∠MGC
∴∠B=∠BEF=60°,∠EFB=180°-∠NFG=60°,NF∥MG,
∴△BEF为等边三角形,四边形NFGM为菱形
∴NF=MG=a,
∴BE=BF=EF=EN+NF=2a,AB=AE+BE=3a,BC=BF+FG+GC=4a
∴EP=BE·sin∠B=![]() ,AD=AB·sin∠B=
,AD=AB·sin∠B=![]() ,FQ=NF·sin∠FNM=
,FQ=NF·sin∠FNM=![]()
由图可知,图中两个阴影部分面积相等
∴![]() =2(S△BEF+S菱形NFGM)
=2(S△BEF+S菱形NFGM)
=2(![]() BF·EP+NM·FQ)
BF·EP+NM·FQ)
=2(![]() ×2a×
×2a×![]() +a·
+a·![]() )
)
=![]()
![]() =BC·AD=4a×
=BC·AD=4a×![]() =
=![]()
∴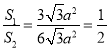
故答案为:![]() .
.


科目:初中数学 来源: 题型:
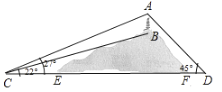
【题目】如图,山顶有一塔![]() ,塔高
,塔高![]() .计划在塔的正下方沿直线
.计划在塔的正下方沿直线![]() 开通穿山隧道
开通穿山隧道![]() .从与
.从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 、
、![]() 的仰角分别为
的仰角分别为![]() 、
、![]() ,从与
,从与![]() 点相距
点相距![]() 的
的![]() 处测得
处测得![]() 的仰角为
的仰角为![]() .求隧道
.求隧道![]() 的长度.(参考数据:
的长度.(参考数据:![]() ,
,![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解高校学生对5G移动通信网络的消费意愿,从在校大学生中随机抽取了1000人进行调查,下面是大学生用户分类情况统计表和大学生愿意为5G套餐多支付的费用情况统计图(例如,早期体验用户中愿意为5G套餐多支付10元的人数占所有早期体验用户的50%).
用户分类 | 人数 |
A:早期体验用户(目前已升级为5G用户) | 260人 |
B:中期跟随用户(一年内将升级为5G用户) | 540人 |
C:后期用户(一年后才升级为5G用户) | 200人 |
下列推断中,不合理的是( )

A.早期体验用户中,愿意为5G套餐多支付10元,20元,30元的人数依次递减
B.后期用户中,愿意为5G套餐多支付20元的人数最多
C.愿意为5G套餐多支付10元的用户中,中期跟随用户人数最多
D.愿意为5G套餐多支付20元的用户中,后期用户人数最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() ,
,![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
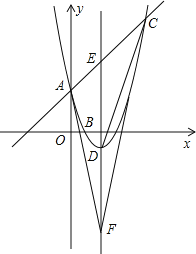
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
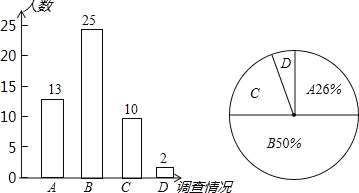
【题目】2015﹣2016年CBA联赛,吉林九台农商行队把长春体育馆作为自己的主场,小球迷“球球”对自己学校部分学生对去赛场为球队加油助威进行了抽样调查,根据收集到的数据绘制了如下的统计图表.(调查情况说明:A:特别愿意去;B:愿意去;C:去不去都行;D:不愿意去)
(1)求出不愿意去的学生的人数占被调查总人数的百分比;
(2)求出扇形统计图中C所在的扇形圆心角的度数;
(3)若该校学生共有2000人,请你估计特别愿意去加油助威的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2+PB2=PC2,则称点P为△ABC关于点C的勾股点.

(1)如图2,在4×3的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点上,请找出所有的格点P,使点P为△ABC关于点A的勾股点.
(2)如图3,△ABC为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)∠PAD=90°,连接DC,DB,求证:点P为△BDC关于点D的勾股点.
(3)如图4,点E是矩形ABCD外一点,且点C是△ABE关于点A的勾股点,若AD=8,CE=5,AD=DE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间,阿里巴巴“爱心助农”计划全面启动,集合天猫、淘宝、聚划算、饿了么、盒马、阿里乡村事业部等,组成了线上线下农产品销售的全域网络,通过这次爱心助农,很多农产品从滞销转变为脱销,以下是某淘宝商家在电商平台上推出的![]() .猕猴桃、
.猕猴桃、![]() .芒果这两种水果,其销售信息如下表:
.芒果这两种水果,其销售信息如下表:
品种 | 销售信息 |
| 5所以内(包含5斤),每斤8元;超过5斤,则超出部分打8折 |
| 3斤以内(包含3斤),每斤10元;超出3斤,所有芒果打9折 |
(1)小佳购买![]() 斤猕猴桃,付款
斤猕猴桃,付款![]() 元,请写出
元,请写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)若小佳购买10斤猕猴桃,小欣购买8斤芒果,比较谁的花费更低?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com