
����Ŀ����֪����x�Ķ��κ���y=ax2-(2a+2)x+b(a��0)��x=0��x=6ʱ����ֵ���.
(1)��a��ֵ;
(2)���ö��κ�����ͼ����ֱ��y=-2x��һ������Ϊ(2,m),�����Ľ���ʽ;
(3)��(2)��������,ֱ��y=-2x-4��x��,y��ֱ���A,B,���߶�AB����ƽ��n(n>0)����λ,ͬʱ���ö��κ�����2��x��7�IJ�������ƽ��n����λ��õ���ͼ���ΪG,����ͼ��ֱ�ӻش�,��ͼ��G��ƽ�ƺ���߶��й�����ʱ,n��ȡֵ��Χ.
���𰸡�(1) x=3,a=![]() (2) y=
(2) y=![]() x2-3x(3)n=1��2��n��4,
x2-3x(3)n=1��2��n��4,
��������
(1)�ɵö��κ���x=3�������a��ֵ��
��2�����������Ϊ(2,-4)�����루1������ʽ�ɵö��κ����Ľ���ʽ��
(3)�������A��B�����꼰ֱ��y=-2x-4����ƽ��n(n>0)����λ�ı���ʽ�����κ�����2��x��7�IJ�������ƽ��n����λ��õ���ͼ���ΪG���ɵ�G�ĺ�������ʽ�����������ķ����н⣬�ɵ�n��ȡֵ��Χ.
(1)�߶��κ�����x=0��x=6ʱ����ֵ���,
��ö��κ����ĶԳ���Ϊx=3
��x=![]() ,
,
�Ⲣ�����:a=![]() .
.
(2)��ֱ��y=-2x����(2,m),
��m=-2��2=-4,
������,��(2,-4)����������,
����(1)a=![]() ,������Ϊy=
,������Ϊy=![]() x2-3x+b,
x2-3x+b,
�ɵ�:2-6+b=-4,
���b=0,
�������ߵĽ���ʽΪy=![]() x2-3x.
x2-3x.
(3)����ͼ��
��n=1ʱ��һ�κ���Ϊ![]() (-1��x��1),GΪ
(-1��x��1),GΪ![]() (1��x��6)���й������㣨1��-4������n=1��������;
(1��x��6)���й������㣨1��-4������n=1��������;
��
��n=2ʱ, ![]() (0��x��2), GΪ
(0��x��2), GΪ![]() (0��x��5), �й������㣨2��-4������n=2��������
(0��x��5), �й������㣨2��-4������n=2��������
��
��n=4ʱ, ![]() (2��x��4), GΪ
(2��x��4), GΪ![]() (-2��x��3),��ʱ�й����㣨2��0��
(-2��x��3),��ʱ�й����㣨2��0��
�ʣ�n=1��2��n��4,


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��6000�ĵ�·�ɼ����������̶Ӹ�����ɣ���֪���̶�ÿ����ɵĹ��������ҹ��̶�ÿ����ɹ�������2�����Ҽ��̶ӵ�����ɴ���̱��ҹ��̶ӵ�����ɴ��������10�죮
��1����ס��������̶�ÿ�����ɶ����ף�
��2��������̶�ÿ���蹤�̷�7000Ԫ���ҹ��̶�ÿ���蹤�̷�5000Ԫ�������ȵ������������죬���ɼ��������̶Ӻ������ʣ�������֧�����̶��ܷ��ò�����79000Ԫ���������̶������Ժ���ʩ�������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ����
����![]() ���ڵ�
���ڵ�![]() ����
����![]() ������һ��
������һ��![]() ������
������![]() .
.

��1������κ����ı���ʽ��
��2������![]() ��������
Ϊ��������![]() �Ḻ�����Ϸ���һ�����㣬��
�Ḻ�����Ϸ���һ�����㣬��![]() ��������ֵ��
��������ֵ��
��3�������߶Գ������Ƿ���ڵ�![]() ��ʹ
��ʹ![]() Ϊ���������Σ������ڣ���ֱ��д������
Ϊ���������Σ������ڣ���ֱ��д������![]() ������꣬����������˵������.
������꣬����������˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
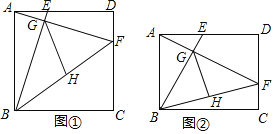
����Ŀ������̽������ͼ�٣���������![]() �У���
�У���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ���߶�
���߶�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��![]() ��
��![]() �����ߣ�
�����ߣ�
��1����֤��![]() ��
��
��2���߶�![]() ��
��![]() ֮���������ϵΪ ��
֮���������ϵΪ ��
������չ����ͼ�ڣ��ھ���![]() �У�
��![]() ��
��![]() ����
����![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ��
��![]() ���߶�
���߶�![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����
����![]() ��
��![]() �����ߣ����߶�
�����ߣ����߶�![]() �ij�Ϊ ��
�ij�Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,AB�ǡ�0��ֱ��,��C�ڡ�0��,D��![]() �е�,����BAC=70��,���C.
�е�,����BAC=70��,���C.
������С���Ľⷨ,�������������:
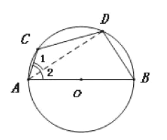
��:�ڡ�0��,
��D��![]() ���е�
���е�
��BD=CD.
���1=��2( )(������������).
�ߡ�BAC=70��,
���2=35��.
��AB�ǡ�0��ֱ��,
���ADB=90��( )(������������).
���B=90��-��2=55��.
��A��B��C��D�ĸ��㶼�ڡ�0��,
���C+��B=180��( )(������������).
���C=180��-��B= (�������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
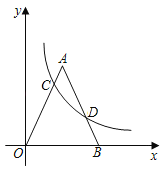
����Ŀ����ͼ��ʾ����ֱ������ϵ�У�OΪԭ�㣬������A0B�Ķ���B��x������AO��AB��A��������(![]() ��5)������������y��
��5)������������y��![]() ��ͼ����AO���ڵ�C����AB���ڵ�D����OC��2BD����k��ֵ��_____��
��ͼ����AO���ڵ�C����AB���ڵ�D����OC��2BD����k��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
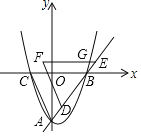
����Ŀ����ͼ��ֱ��![]() ��x�ύ�ڵ�B����y�ύ�ڵ�A��������
��x�ύ�ڵ�B����y�ύ�ڵ�A��������![]() ����A��B���㣬��x�����һ����ΪC��
����A��B���㣬��x�����һ����ΪC��
��1���������ߵĽ���ʽ��
��2������ABC��ÿ��1����λ���ٶ�������AB����ƽ�ƣ�ƽ�ƺ�������μ�Ϊ��DEF��ƽ��ʱ��Ϊt�룬0��t��5��ƽ�ƹ�����EF�������߽��ڵ�G��
�ٵ�FG��GE��3��2ʱ����t��ֵ��
����DEF����AOB�ص��������ΪS��ֱ��д��S��t�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ���ı���ABCD������AB��AD�ij��ǹ���x�ķ���x2��mx+![]() ��
��![]() ��0������ʵ������
��0������ʵ������
��1��mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ôABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
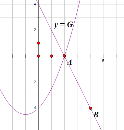
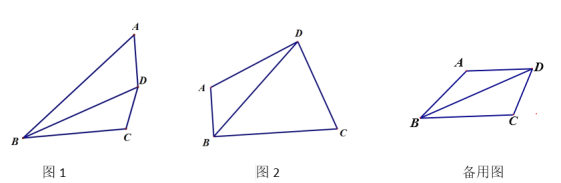
����Ŀ�����ı��� ABCD �У�BD ƽ�֡�ABC��
��1����ͼ 1������BAD=��BDC����֤��BD2=ABBC��
��2����ͼ 2����A>90������BAD+��BDC=180����
������ABC=90�㣬AB=![]() ��BC=8����BD�ij���
��BC=8����BD�ij���
���� BC=3CD=3a��BD=9�� �� AB �ij�Ϊ �� (�ú� a �Ĵ���ʽ��ʾ)��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com