
分析 先根据分式混合运算的法则把原式进行化简,再根据$\frac{1}{x}$-$\frac{1}{y}$=4,xy=-1求出$\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$=14,$\frac{1}{x}$+$\frac{1}{y}$=2$\sqrt{3}$,代入原式进行计算即可.
解答 解:∵$\frac{1}{x}$-$\frac{1}{y}$=4,xy=-1,
∴($\frac{1}{x}$-$\frac{1}{y}$)2=16,
∴$\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$=16-2=14,$\frac{1}{x}$+$\frac{1}{y}$=$\sqrt{{(\frac{1}{x}-\frac{1}{y})}^{2}+\frac{4}{xy}}$=$\sqrt{16-4}$=2$\sqrt{3}$,
∴原式=($\frac{1}{{x}^{2}}$-$\frac{1}{{y}^{2}}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)
=($\frac{1}{x}$+$\frac{1}{y}$)($\frac{1}{x}$-$\frac{1}{y}$)($\frac{1}{{x}^{2}}$+$\frac{1}{{y}^{2}}$)
=2$\sqrt{3}$×4×14
=112$\sqrt{3}$.
故答案为:112$\sqrt{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
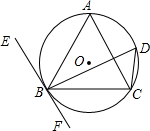 如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=$\sqrt{3}$cm.
如图,已知△ABC内接于⊙O,过点B作直线EF∥AC,又知∠ACB=∠BDC=60°,AC=$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
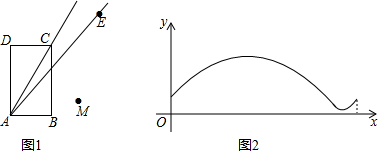
| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com