
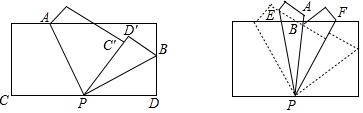
分析 (1)根据折叠的性质,可得∠APC'=$\frac{1}{2}$∠CPC',∠BPD'=$\frac{1}{2}$∠DPD',再根据角的和差关系进行计算,可得∠APB=∠APC'+∠BPD'=90°;
(2)根据折叠的性质,可得∠APE=$\frac{1}{2}$∠APG,∠BPF=$\frac{1}{2}$∠APH,再根据角的和差关系进行计算,可得∠EPF=∠APE+∠BPF=45°.
解答 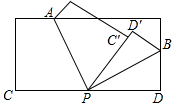 解:(1)如图所示,由折叠得,∠APC'=$\frac{1}{2}$∠CPC',∠BPD'=$\frac{1}{2}$∠DPD',
解:(1)如图所示,由折叠得,∠APC'=$\frac{1}{2}$∠CPC',∠BPD'=$\frac{1}{2}$∠DPD',
∴∠APB=∠APC'+∠BPD'
=$\frac{1}{2}$∠CPC'+$\frac{1}{2}$∠DPD'
=$\frac{1}{2}$(∠CPC'+∠DPD')
=$\frac{1}{2}$×180°
=90°;
(2)如图所示,由折叠得,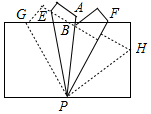 ∠APE=$\frac{1}{2}$∠APG,∠BPF=$\frac{1}{2}$∠APH,
∠APE=$\frac{1}{2}$∠APG,∠BPF=$\frac{1}{2}$∠APH,
∴∠EPF=∠APE+∠BPF
=$\frac{1}{2}$∠APG+$\frac{1}{2}$∠APH
=$\frac{1}{2}$(∠APG+∠APH)
=$\frac{1}{2}$×∠GPH
=$\frac{1}{2}$×90°
=45°.
故答案为:45°.
点评 本题主要考查了矩形的性质以及折叠的性质的综合应用,解决问题的关键是掌握:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
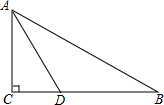 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,交BC于点D,若CD=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
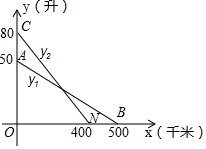 如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.
如图,线段AB、CD分别是一辆轿车的邮箱剩余油量y1(升)与另一辆客车的邮箱剩余油量y2(升)关于行驶路程x(千米)的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
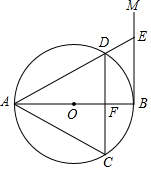 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且$\widehat{DA}$=$\widehat{DC}$,连接AC,AD,延长AD交BM于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
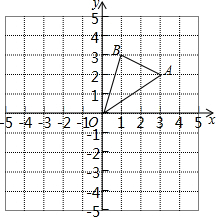 如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.
如图,△AOB的顶点均在格点上,每个小正方形的边长均为1个单位长度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com