
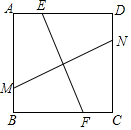
 如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.
如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.分析 过F作FP⊥AD,过N作NQ⊥AB,交于点H,分两种情况证明△MNQ≌Rt△EFP后,利用全等三角形的性质即可判断.
解答 解:过F作FP⊥AD,过N作NQ⊥AB,交于点H
∵正方形ABCD,
∴AB=BC=CD=AD,∠A=∠D=∠B=∠C=90°,
∴四边形AQND和四边形PFCD都为矩形,
∴QN=PF=CD=AD,
①若MN=EF,
在Rt△MNQ和Rt△EFP中,
$\left\{\begin{array}{l}{MN=EF}\\{QN=PF}\end{array}\right.$,
∴Rt△MNQ≌Rt△EFP(HL),
∴∠QNM=∠PFE,
∵∠FHN=90°,
∴MN⊥EF,
若EF如右图所示时,此时EF与MN不垂直
故①不正确;
②若MN⊥EF,∠FHN=90°
∴∠QNM=∠PFE,
在Rt△MNQ和Rt△EFP中,
$\left\{\begin{array}{l}{∠MNQ=∠EFP}\\{∠MQN=∠EPF}\\{QN=PF}\end{array}\right.$
∴Rt△MNQ≌Rt△EFP(AAS),
∴MN=EF
故②正确,
故答案为:②
点评 本题考查正方形的性质,涉及全等三角形的性质与判定,分类讨论的思想,属于中等题型.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:填空题
 如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′=3$\sqrt{2}$.
如图,△ABC是等腰直角三角形,BC是斜边,将△ABP绕点A逆时针旋转后,能与△ACP′重合,如果AP=3,那么PP′=3$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
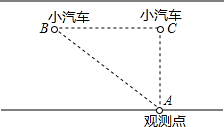 “中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路上的行驶速度不能低于60千米/小时不得超过120千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到观测点A正前方60米处,过了3秒后,测得小汽车与观测点间的距离变为100米.这辆小汽车行驶速速度符合规定吗?(在横线上填序号①符合 ②不符合)①.
“中华人民共和国道路交通管理条例”规定:小汽车在沿海高速路上的行驶速度不能低于60千米/小时不得超过120千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到观测点A正前方60米处,过了3秒后,测得小汽车与观测点间的距离变为100米.这辆小汽车行驶速速度符合规定吗?(在横线上填序号①符合 ②不符合)①.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y值随着x值的增大而减小 | B. | 图象是双曲线,是中心对称图形 | ||
| C. | 当x>l时,0<y<l | D. | 图象可能与坐标轴相交 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com