
【题目】正△ABC的边长为4,⊙A的半径为2,D是⊙A上动点,E为CD中点,则BE的最大值为____.
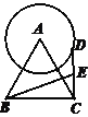
【答案】![]()
【解析】
延长CB到点F,使FB=BC=4,连接AF,过点A作AH⊥FC于点H,找出点F与⊙A上距离最近、最远的点,即可得出DF的取值范围,从而求出最大值,再根据BE是△CDF的中位线即可解答.
解:如图:延长CB到点F,使FB=BC=4,连接AF,过点A作AH⊥FC于点H,
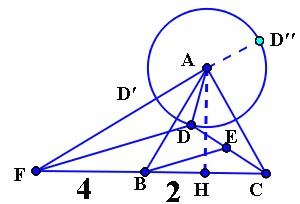
又∵正△ABC的边长为4,
∴AH=2![]() ,BH=2,
,BH=2,
在Rt△AFH中,由勾股定理易得AF=![]() =4
=4![]()
∵E为CD中点,
∴BE∥DF,BE=![]() DF
DF
当点D与D′重合时,FD最小此时FD=4![]() -2;当点D与D′′重合时,FD最大,此时FD=4
-2;当点D与D′′重合时,FD最大,此时FD=4![]() +2,即AF-AD≤FD≤AF+AD
+2,即AF-AD≤FD≤AF+AD
∴BE的最大值为![]() ( 4
( 4![]() +2)=
+2)=![]() .
.
故答案为:![]() .
.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
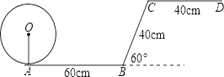
【题目】一位小朋友在粗糙不打滑的“Z”字形平面轨道上滚动一个半径为10cm的圆盘,如图所示,AB与CD是水平的,BC与水平面的夹角为60°,其中AB=60cm,CD=40cm,BC=40cm,那么该小朋友将圆盘从A点滚动到D点其圆心所经过的路线长为___________cm
查看答案和解析>>
科目:初中数学 来源: 题型:
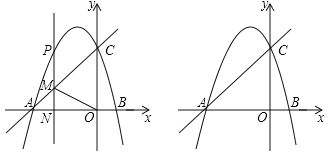
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=
x2+bx+c与x轴交于A、B两点,与y轴交于C.直线y=![]() x+3经过点A、C.
x+3经过点A、C.
(1)求抛物线的解析式;
(2)P是抛物线上一动点,过P作PM∥y轴交直线AC于点M,设点P的横坐标为t.
①若以点C、O、M、P为顶点的四边形是平行四边形,求t的值.
②当射线MP,AC,MO中一条射线平分另外两条射线的夹角时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
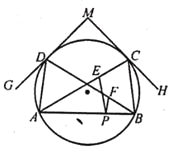
【题目】如图,⊙O的半径为4,A,B,C,D是⊙O上的四点,过点C,D的切线CH,DG相交于点M,点P在弦AB上,PE∥BC交AC于点E,PF∥AD于点F,当∠ADG=∠BCH=30°时,PE+PF的值是( )
A. 4B. 2 ![]() C. 4
C. 4 ![]() D. 不确定
D. 不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
(2) 求证:∠ACF=90°;
(3) 连接AF,过A,E,F三点作圆,如图2. 若EC=4,∠CEF=15°,求![]() 的长.
的长.

图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
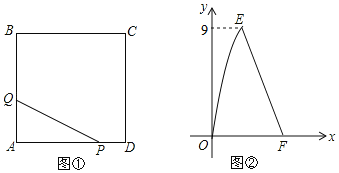
【题目】如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动:同时点Q沿边AB,BC从点A开始向点C以acm/s的速度移动,当点P移动到点A时,P,Q同时停止移动.设点P出发x秒时,△PAQ的面积为ycm2,y与x的函数图象如图②,线段EF所在的直线对应的函数关系式为y=﹣4x+21,则a的值为( )
A. 1.5B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=![]() 的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
的一个分支上,过C点的直线y=﹣x+b与双曲线的另一个交点为E,则△EOC的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级10个班的300名学生即将参加学校举行的研究旅行活动,学校提出以下4个活动主题:A.赤水丹霞地貌考察;B.平塘天文知识考察;C.山关红色文化考察;D.海龙电土司文化考察,为了解学生喜欢的活动主题,学生会开展了一次调查研究,请将下面的过程补全
(1)收集数据:学生会计划调查学生喜欢的活动主题情况,下面抽样调查的对象选择合理的是______.(填序号)
①选择七年级3班、4班、5班学生作为调查对象
②选择学校旅游摄影社团的学生作为调查对象
③选择各班学号为6的倍数的学生作为调查对象
(2)整理、描述数据:通过调査后,学生会同学绘制了如下两幅不完整的统计图,请把统计图补充完整
某校七年级学生喜欢的活动主题条形统计图某校七年级学生喜欢的活动主题扇形统计图
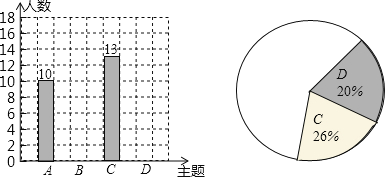
(3)分析数据、推断结论:请你根据上述调查结果向学校推荐本次活动的主题,你的推荐是______(填A-D的字母代号),估算全年级大约有多少名学生喜欢这个主题活动
(4)若在5名学生会干部(3男2女)中,随机选取2名同学担任活动的组长和副组长,求抽出的两名同学恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
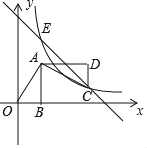
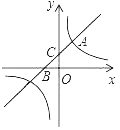
【题目】如图,直线y=x+b与双曲线y=![]() (k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(k为常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.
(1)求直线和双曲线的解析式;
(2)点P在x轴上,且△BCP的面积等于2,求P点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com