
 ��ͼ����֪һ�κ���y=$\frac{1}{2}$x+1��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B�����κ���y=$\frac{1}{2}$x2+bx+c��ͼ����һ�κ���y=$\frac{1}{2}$x+1��ͼ���ڵ�B��C���㣬��x�ύ��D��E���㣬��D������Ϊ��1��0����
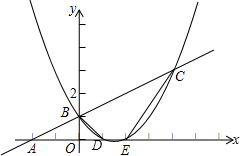
��ͼ����֪һ�κ���y=$\frac{1}{2}$x+1��ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B�����κ���y=$\frac{1}{2}$x2+bx+c��ͼ����һ�κ���y=$\frac{1}{2}$x+1��ͼ���ڵ�B��C���㣬��x�ύ��D��E���㣬��D������Ϊ��1��0�������� ��1������һ�κ����Ľ���ʽ���ҳ���B�����꣬�ٸ��ݵ�A��D���������ô���ϵ��������������κ����Ľ���ʽ��
��2��������ڣ����P������Ϊ��t��0��������ֱ���������߽���ʽ�ɷ����飬�ⷽ���������C�����꣬���ݵ�B��P���������������ľ��빫ʽ�������PB��PC��BC�ij��ȣ������ù��ɶ������ɵó�����t��һԪ���η��̣��ⷽ�̼��ɵó����ۣ�
��3��������ڣ���AP=2t��AQ=at����һ�κ�������ʽ�����ҳ���A�����꣬��ϵ�B��D�����꼴�ɵó�AB��AD�ij��ȣ��֡�PAQ��BAD�͡�PAQ�ס�DAB����������ǣ��������������ε����ʼ��ɵó�����a��һԪһ�η��̣��ⷽ�̼������aֵ������ý⣮
��� �⣺��1����x=0ʱ��y=1��
��B��0��1����
����B��0��1����D��1��0������y=$\frac{1}{2}$x2+bx+c��
$\left\{\begin{array}{l}{c=1}\\{\frac{1}{2}+b+c=0}\end{array}\right.$����ã�$\left\{\begin{array}{l}{b=-\frac{3}{2}}\\{c=1}\end{array}\right.$��
����κ����Ľ���ʽΪy=$\frac{1}{2}$x2-$\frac{3}{2}$x+1��
��2��������ڣ����P������Ϊ��t��0����
����ֱ��AB�������ߵĽ���ʽ�ɷ����飬
$\left\{\begin{array}{l}{y=\frac{1}{2}x+1}\\{y=\frac{1}{2}{x}^{2}-\frac{3}{2}x+1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=0}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=4}\\{{y}_{2}=3}\end{array}\right.$��
���C��������4��3����
��B��0��1����P��t��0����
��BC=2$\sqrt{5}$��CP=$\sqrt{��4-t��^{2}+��3-0��^{2}}$=$\sqrt{{t}^{2}-8t+25}$��BP=$\sqrt{��t-0��^{2}+��0-1��^{2}}$=$\sqrt{{t}^{2}+1}$��
����Rt��PBC�У���BPC=90�㣬
��BC2=CP2+BP2����20=t2-8t+25+t2+1��
��ã�t1=1��t2=3��
�ʴ��ڶ���P��ʹ�á�PBC����PΪֱ�Ƕ����ֱ�������Σ���ʱ��P�˶���ʱ��Ϊ1���3�룮
��3��������ڣ���AP=2t��AQ=at��
��y=0ʱ��x=-2��
��A��-2��0����
��B��0��1����D��1��0����
��AB=$\sqrt{5}$��AD=3��
�ߡ�PAQ=��BAD��
����A��P��Q��������������ABD���������������
�ٵ���PAQ��BADʱ����$\frac{AP}{AB}=\frac{AQ}{AD}$����$\frac{2t}{\sqrt{5}}=\frac{at}{3}$��
��ã�a=$\frac{6\sqrt{5}}{5}$��
�ڵ���PAQ�ס�DABʱ����$\frac{AP}{AD}=\frac{AQ}{AB}$����$\frac{2t}{3}=\frac{at}{\sqrt{5}}$��
��ã�a=$\frac{2\sqrt{5}}{3}$��
���Ͽ�֪��������A��P��QΪ��������������ABD���ƣ�a��ֵΪ$\frac{6\sqrt{5}}{5}$��$\frac{2\sqrt{5}}{3}$��
���� ���⿼����һ�κ���ͼ���ϵ����������������ϵ������������ʽ�����ɶ����Լ����������ε����ʣ�����Ĺؼ��ǣ���1�����ô���ϵ����������κ�������ʽ����2�����ù��ɶ����ҳ�����t��һԪ���η��̣���3���֡�PAQ��BAD�͡�PAQ�ס�DAB����������ǣ����������е��⣬�ѶȲ������������Ŀʱ�����ݵ���������ô���ϵ���������������ʽ�ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����������IJ�һ��С�ڱ����� | B�� | -aһ���Ǹ��� | ||
| C�� | ��������������ֵ��ķ���С | D�� | �����������ĺ�һ�����ڼ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 125�� | C�� | 250�� | D�� | 499�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A������ԭ��O�غϣ�B��4��0����D��0��3������E�ӵ�A������������AB�ƶ�����CEΪֱ������M����FΪ��M������DB�Ĺ����㣬����EF��CF������E��EG��EF��EG���M�ཻ�ڵ�G������CG��
��ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A������ԭ��O�غϣ�B��4��0����D��0��3������E�ӵ�A������������AB�ƶ�����CEΪֱ������M����FΪ��M������DB�Ĺ����㣬����EF��CF������E��EG��EF��EG���M�ཻ�ڵ�G������CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
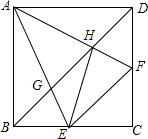 ��ͼ��������ABCD�У���E��F�ֱ���BC��DC�ϣ���EAF=45�㣬AE��AF�ֱ�BD��G��H�����н���
��ͼ��������ABCD�У���E��F�ֱ���BC��DC�ϣ���EAF=45�㣬AE��AF�ֱ�BD��G��H�����н���| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com