
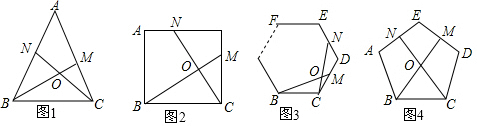
分析 (1)①正三角形ABC中,可通过全等三角形来证明BM=CN,由于∠BON=∠MBC+∠BCO=60°,而∠ACB=∠ACN+∠OCB=60°,因此∠ACN=∠MBC,又知道∠A=∠BCM=60°,AC=BC,因此△ACN≌△CBM,可得出BM=CN;②同①;
(2)①由(1)的证明过程可知道∠MON的度数应该是正多边形的内角的度数,当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立,
②可参照(1)先得出三角形BCD和CDE全等,然后通过证三角形CEN和BDM全等来得出结论,在证三角形CEN和BDM全等的过程中也是通过∠BON与正五边形的内角相等得出一组对应角相等,然后根据正五边形的内角减去第一对全等三角形中得出的相等角来得出另一组对应角相等,可通过△BCD≌△CDE得出CE=BD,那么可得出三角形CEN和BDM全等,由此可得证.
解答 解:(1)选命题①
在图1中,∵△ABC是正三角形,
∴BC=CA,∠BCM=∠A=60°.
∵∠BON=60°,
∴∠CBM+∠BCN=60°.
∵∠BCN+∠ACN=60°,
∴∠CBM=∠ACN.
在△BCM和△CAN中,$\left\{\begin{array}{l}{∠BCM=∠A}&{\;}\\{BC=CA}&{\;}\\{∠CBM=∠ACN}&{\;}\end{array}\right.$,
∴△BCM≌△CAN(ASA).
∴BM=CN.
选命题②
在图2中∵四边形ABCD是正方形,
∴BC=CD,∠BCM=∠D=90°.
∵∠BON=90°,
∴∠CBM+∠BCN=90°.
∵∠BCN+∠DCN=90°,
∴∠CBM=∠DCN.
在△BCM和△CAN中,$\left\{\begin{array}{l}{∠BCM=∠D}&{\;}\\{BC=CD}&{\;}\\{∠CBM=∠DCN}&{\;}\end{array}\right.$,
∴△BCM≌△CDN(ASA).
∴BM=CN.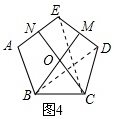
(2)①当∠BON=$\frac{(n-2)×180°}{n}$时,结论BM=CN成立.
②BM=CN成立.理由如下:
在图4中,连接BD、CE,
∵五边形ABCDE是正五边形,
∴BC=CD=DE,∠BCD=∠CDE=108°,∠DEA=108°.
在△BCD和△CDE中,$\left\{\begin{array}{l}{BC=CD}&{\;}\\{∠BCD=∠CDE}&{\;}\\{CD=DE}&{\;}\end{array}\right.$,
∴△BCD≌△CDE(SAS).
∴BD=CE,∠BDC=∠CED,∠DBC=∠ECD.
∵∠BON=108°,
∴∠OBC+∠OCB=108°.
∵∠OCB+∠OCD=108°,
∴∠OBC=∠OCD(即∠MBC=∠NCD).
∴∠MBC-∠DBC=∠NCD-∠ECD,即∠DBM=∠ECN.
∴∠CDE-∠BDC=∠DEA-∠CED,即∠BDM=∠CEN.
在△BDM和△CEN中,$\left\{\begin{array}{l}{∠BDM=∠CEN}&{\;}\\{BD=CE}&{\;}\\{∠DBM=∠ECN}&{\;}\end{array}\right.$,
∴△BDM≌△CEN(ASA).
∴BM=CN.
点评 本题是四边形综合题目,考查了等边三角形的性质,正方形的性质,全等三角形的判定与性质,正多边形等几何知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
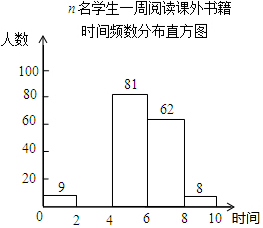 某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.
某校为了解“书香校园”活动的开展情况,随机抽取了n名学生,调查他们一周阅读课外书籍的时间(单位:时),并将所得数据绘制成如下的统计图表.| 时间段 | 频数 |
| 0<t≤2 | 9 |
| 2<t≤4 | 40 |
| 4<t≤6 | 81 |
| 6<t≤8 | 62 |
| 8<t≤10 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
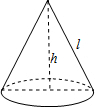 如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )
如图是一顶圆锥形烟囱小纸帽,它的母线长l是13cm,高h为12cm,则制作这顶纸帽所需纸张的面积是(接缝忽略不计)( )| A. | 60π | B. | 65π | C. | 78π | D. | 156π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com