Question

如图，在等腰三角形ABC中，AB=AC=10cm，∠ABC=30⁰，以BC所在直线为x轴，以BC边上的高所在的直线为y轴建立平面直角三角形系。

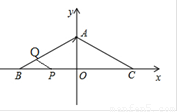
（1）求直线AC的解析式；

（2）有一动点P以1cm/s的速度从点B开始沿x轴向其正方向运动，设点P的运动为t秒（单位：s）。

①当t为何值时，ΔABP是直角三角形；

②现有另一点Q与点P同时从点B开始，以1cm/s的速度从点B开始沿折线BAC运动，当点Q到达点C时，P、Q两点同时停止运动。试写出ΔBPQ的面积S关于t的函数解析式，并写出自变量的取值范围。

 

Answer 1

【答案】

（1）y=-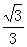x+5  （2）t=5；t=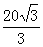

（3）当0<t<10时，S=t²；10<t≤20时，S=-t²+5t

【解析】

试题分析：（1）AC=10，∠ABC=30⁰因为是等腰三角形ABC，所以OA="5" ，从而可得到OC=5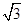.那么A(0，5),C(5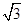,0),设直线AC的解析式为y=ax+b，代入A,C两点，得y=-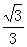x+5

（2）ΔABP是直角三角形也即p点运动到0点，即运动的距离为线段BO，BO=OC。所以运动的时间为5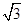s

当∠BAP=90⁰时，此时的P点在X轴的正半轴。此时的p点可设为（x,0）,由题可得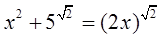,即X=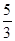,加上前面的5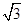，得到t=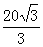

（3）0<t<10，即Q在BA点运动时，S=txtx=

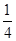
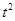
10<t≤20,Q在AC上运动，设此时Q的坐标为（m,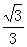m+5）,再由5-(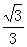m+5)=(t-10)x得出Q点的纵坐标为10-t,围成的三角形面积=tx(10-t )x=-t²+5t

考点：函数的解析式的求法，三角形的面积。

点评：此题较难。有很强的综合性。要求考生基础扎实，对问题有较强的分析能力。