
【题目】某校开展以“我们都是追梦人”为主题的校园文化节活动,活动分为球类、书画、乐器、诵读四项内容,要求每位学生参加其中的一项.校学生会为了解各项报名情况,随机抽取了部分学生进行调查,并对调查结果进行了统计,绘制了如下统计图(均不完整):

请解答以下问题:
(1)图1中,“书画”这一项的人数是 .
(2)图2中,“乐器”这一项的百分比是 ,“球类”这一项所对应的扇形的圆心角度数是 .
(3)若该校共有2200名学生,请估计该校参加“诵读”这一项的学生约有多少人.
【答案】(1)30;(2)10%;108°;(3)约有880人
【解析】
(1)根据条形图得到参加诵读活动的人数,根据扇形图得到参加诵读活动的人数所占的百分比,从而求出抽取的学生总数,根据“书画”这一项的百分比计算,得到答案;
(2)根据条形图得到“乐器”这一项的人数、“球类”这一项的人数,求出“乐器”这一项的百分比、“球类”这一项所对应的扇形的圆心角度数;
(3)根据参加诵读活动的人数占40%,估计总体,得到答案.
解:(1)由条形图可知,参加诵读活动的人数为60,
由扇形图可知,参加诵读活动的人数占40%,
∴抽取的学生数为:60÷40%=150(人),
∴“书画”这一项的学生数是:150×20%=30(人),
故答案为:30;
(2)“乐器”这一项的百分比是:15÷150×100%=10%,
“球类”这一项所对应的扇形的圆心角度数是:![]() ×360°=108°,
×360°=108°,
故答案为:10%;108°;
(3)该校参加“诵读”这一项的学生约有:2200×40%=880(人),
答:该校参加“诵读”这一项的学生约有880人.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.
(1)甲,乙两公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“过直线外一点作已知直线的平行线”的尺规作图过程.
已知:直线![]() 及直线
及直线![]() 外一点P.
外一点P.

求作:直线![]() ,使
,使![]() .
.
作法:如图,

①在直线![]() 上取一点O,以点O为圆心,
上取一点O,以点O为圆心,![]() 长为半径画半圆,交直线
长为半径画半圆,交直线![]() 于
于![]() 两点;
两点;
②连接![]() ,以B为圆心,
,以B为圆心,![]() 长为半径画弧,交半圆于点Q;
长为半径画弧,交半圆于点Q;
③作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小明设计的尺规作图过程:
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明
证明:连接![]() ,
,
∵![]() ,
,
∴![]() __________.
__________.
∴![]() (______________)(填推理的依据).
(______________)(填推理的依据).
∴![]() (_____________)(填推理的依据).
(_____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足![]() ,则称点P为⊙O的“随心点”.
,则称点P为⊙O的“随心点”.

(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(![]() ,2),D(
,2),D(![]() ,
,![]() )中,⊙O的“随心点”是 ;
)中,⊙O的“随心点”是 ;
(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;
(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究.
如图1,抛物线y=![]() x2﹣
x2﹣![]() x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
x﹣2与x轴交于A,B两点,与y轴交于点C,经过点B的直线交y轴于点E(0,2).
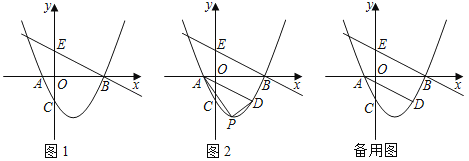
(1)求A,B,C三点的坐标及直线BE的解析式.
(2)如图2,过点A作BE的平行线交抛物线于点D,点P是抛物线上位于线段AD下方的一个动点,连接PA,PD,求OAPD面积的最大值.
(3)若(2)中的点P为抛物线上一动点,在x轴上是否存在点Q,使得以A,D,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交AE的延长线于点F,连接BF.

(1) 求证:CF=AD;
(2) 若CA=CB,∠ACB=90°,试判断四边形CDBF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于点G,BG=4![]() ,则△EFC的周长为( )
,则△EFC的周长为( )
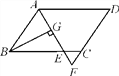
A. 11 B. 10 C. 9 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com