
【题目】![]() 某校为了解七、八年级学生对“新冠”传播与防治知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理和分析.部分信息如下:
某校为了解七、八年级学生对“新冠”传播与防治知识的掌握情况,从七、八年级各随机抽取50名学生进行测试,并对成绩(百分制)进行整理和分析.部分信息如下:
a.七年级成绩频数分布直方图:
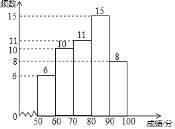
b.七年级成绩在70![]() m
m![]() 80这一组的是:
80这一组的是:
70,72,72,75,76,76,77,77,78,79,79
c.七、八年级成绩的平均数、中位数如下:
年级 | 平均数 | 中位数 |
七 | 76.9 | a |
八 | 79.2 | 79.5 |
根据以上信息,回答下列问题:
(1)在这次测试中,七年级在70分以上的有 人,表格中a的值为 ;
(2)在这次测试中,七年级学生甲与八年级学生乙的成绩都是79分,请判断两位学生在各自年级的排名谁更靠前;
(3)该校七年级学生有500人,假设全部参加此次测试,请你估计七年级成绩超过平均数76.9分的人数.
【答案】(1)33,78.5;(2)在这次测试中,七年级学生甲在本年级的排名谁更靠前;(3)七年级成绩超过平均数76.9分的有280人
【解析】
(1)根据频数分布表中的数据可以得到在这次测试中,七年级在70分以上的人数;根据统计图和统计表中的数据和七年级成绩在70≤x<80这一组的数据,可以求得a的值;
(2)根据统计表中的数据可以得到两位学生在各自年级的排名谁更靠前;
(3)根据统计图中的数据和题目中的数据可以计算出七年级成绩超过平均数76.9分的人数.
解:(1)在这次测试中,七年级在70分以上的有:10+15+8=33(人),
七年级抽查了50名学生,
∴a=(78+79)÷2=78.5,
故答案为:33,78.5;
(2)∵七年级的中位数是78.5,八年级的中位数是79.5,
79>78.5,79<79.5,
∴在这次测试中,七年级学生甲在本年级的排名谁更靠前;
(3)500×![]() =280(人);
=280(人);
答:七年级成绩超过平均数76.9分的有280人.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
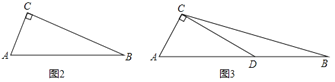
【题目】如图,平面内的两条直线l1、l2,点A、B在直线l2上,过点A、B两点分别作直线l1的垂线,垂足分别为A1、B1,我们把线段A1B1叫做线段AB在直线l2上的正投影,其长度可记作T(AB,CD)或T(AB,l2),特别地,线段AC在直线l2上的正投影就是线段A1C,请依据上述定义解决如下问题.
(1)如图1,在锐角△ABC中,AB=5,T(AC,AB)=3,则T(BC,AB)= ;
(2)如图2,在Rt△ABC中,∠ACB=90°,T(AC,AB)=4,T(BC,AB)=9,求△ABC的面积;
(3)如图3,在钝角△ABC中,∠A=60°,点D在AB边上,∠ACD=90°,T(AD,AC)=2,T(BC,AB)=6,求T(BC,CD).

查看答案和解析>>
科目:初中数学 来源: 题型:
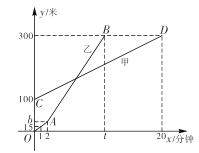
【题目】甲、乙二人都是户外运动爱好者,在一次登山活动中,甲、乙二人距出发点的高度![]() (单位:米),
(单位:米),![]() (单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(单位:米)与乙登山时间 x (单位:分钟)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山的速度是每分钟 米,乙在 2 分钟时提速,提速时距地面的高度![]() 为______米;
为______米;
(2)若乙提速后,乙的速度是甲登山速度的 3 倍,请分别求出甲、乙二人登山全过程中,登山时距地面的高度![]() ,
, ![]() 与乙登山时间
与乙登山时间![]() 之间的函数关系式;
之间的函数关系式;
(3)在(2)的条件下,乙登山多长时间追上了甲? 此时乙距提速时的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的边AB是⊙O的直径,点C在⊙O上,已知AC=6cm,BC=8cm,点P、Q分别在边AB、BC上,且点P不与点A、B重合,BQ=kAP(k>0),联接PC、PQ.
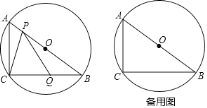
(1)求⊙O的半径长;
(2)当k=2时,设AP=x,△CPQ的面积为y,求y关于x的函数关系式,并写出定义域;
(3)如果△CPQ与△ABC相似,且∠ACB=∠CPQ,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
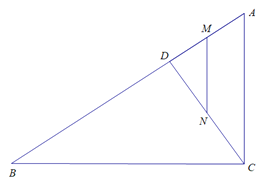
【题目】如图,在Rt⊿ABC中,∠ACB是直角, tan∠B=![]() ,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动,到达点B即停止,M、N分别是AD、CD的中点,连结MN,设点D的运动时间为t
,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动,到达点B即停止,M、N分别是AD、CD的中点,连结MN,设点D的运动时间为t
(1)求MN的长;
(2)求点D由点A到点B匀速运动过程中,线段MN所扫过的面积;
(3)若⊿DMN是等腰三角形时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点的左侧),与
点的左侧),与![]() 轴相交于
轴相交于![]() 点,且
点,且![]() .
.

(1)求这条抛物线的解析式;
(2)如图2,![]() 点在
点在![]() 轴上,且在
轴上,且在![]() 点的右侧,
点的右侧,![]() 点为抛物线上第二象限内的点,连接
点为抛物线上第二象限内的点,连接![]() 交抛物线于第二象限内的另外一点
交抛物线于第二象限内的另外一点![]() ,点
,点![]() 到
到![]() 轴的距离与点
轴的距离与点![]() 到
到![]() 轴的距离之比为
轴的距离之比为![]() ,已知
,已知![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图3,在(2)的条件下,点![]() 由
由![]() 出发,沿
出发,沿![]() 轴负方向运动,连接
轴负方向运动,连接![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,与抛物线相交于点
,与抛物线相交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
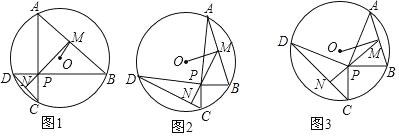
【题目】点P为⊙O内一点,A、B、C、D为圆上顺次四个点,连接AB、CD,OM⊥AB于点M,连接MP并延长交CD于点N,连接PA、PB、PC、PD.
(1)如图1,若A、P、C三点共线,B、P、D三点共线,且AC⊥BD,求证:PN⊥CD;
(2)如图2,若PA=PD,PA⊥PD,PC=PB,PC⊥PB,求证:PN⊥CD;
(3)如图3,在(2)的条件下,PA=10,PC=6,∠APB=60°,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其对称轴为直线
点,其对称轴为直线![]() .
.
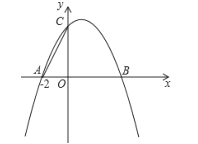
(1)直接写出抛物线的解析式;
(2)把线段![]() 沿
沿![]() 轴向右平移,设平移后
轴向右平移,设平移后![]() 、
、![]() 的对应点分别为
的对应点分别为![]() 、
、![]() ,当
,当![]() 落在抛物线上时,求
落在抛物线上时,求![]() 、
、![]() 的坐标;
的坐标;
(3)除(2)中的平行四边形![]() 外,在
外,在![]() 轴和抛物线上是否还分别存在点
轴和抛物线上是否还分别存在点![]() 、
、![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,求出
为顶点的四边形为平行四边形?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com