
阅读(1)的推导并填空,然后解答第(2)题。
当,![]()
又![]() ,
,
![]() ,
,![]()
即:无论x怎样变化,![]() 的所有取值中,以A为最大;且在
的所有取值中,以A为最大;且在![]() 时,
时,![]() 的值等于A,其中,用
的值等于A,其中,用![]() 表示,A=_______________,B=_______________;
表示,A=_______________,B=_______________;
(2
)为了绿化城市,我市准备在如图的矩形ABCD内规划一块地面,修建一个矩形草坪PQRC。按计划要求,草坪的两边RC与CP分别在BC和CD上,且草坪不能超过文物保护区△AEF的边界EF。经测量知,AB=CD=100m,BC=AD=80m,AE=30m,AF=20m。应如何确定草坪的位置,才能使草坪占地面积最大又符合设计要求?并求出这个最大面积(结果保留到个位,解答时可应用(1)的结论)。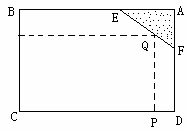
 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:阅读理解
| n(n-1) |
| 2 |
| 点的个数 | 可连成的三角形的个数 | ||||
| 3 | 1 1 | ||||
| 4 | 4 4 | ||||
| 5 | 10 10 | ||||
| … | … | ||||
| n |
|
| n(n-1)(n-2) |
| 6 |
| n(n-1)(n-2) |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 .
.| 点的个数 | 可连成的三角形的个数 |
| 3 | ________ |
| 4 | ________ |
| 5 | ________ |
| … | … |
| n | ________ |
查看答案和解析>>
科目:初中数学 来源:江苏期末题 题型:解答题
 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下列材料,完成材料后问题
课本上推导两个数和完全平方公式给出几何意义,利用图形的面积解释。
 如图1,一个边长为
如图1,一个边长为![]() 的正方形可以看做由
的正方形可以看做由
 边长为
边长为![]() 的正方形和边长为
的正方形和边长为![]() 的正方形以及长宽分别为
的正方形以及长宽分别为![]() 的两个长方形构成。
的两个长方形构成。
即边长为![]() 的正方形的面积有两种算法:
的正方形的面积有两种算法:![]() 以及
以及![]() ,由此得到了一个等式:
,由此得到了一个等式: ![]() 。由此发现可以利用几何解释代数中的公式。请你参考课本上做法类比的解决下列问题:
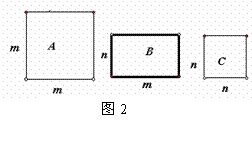
。由此发现可以利用几何解释代数中的公式。请你参考课本上做法类比的解决下列问题:
现有三种不同类型的长方形地砖长宽如图2所示。若现有A类4块,B类4块,C类2块,请问这些地砖的总面积为_______________________.如果用现有的地砖要拼成一个正方形,则多余1块___________型地砖(填A,B,C);这样的地砖拼法也表示了一个两数和的平方的几何意义,请你用含有![]() 的等式写出这两个数的和的平方_________________,并类比阅读材料画图利用所给地砖,画图用图形面积给予几何直观的解释.
的等式写出这两个数的和的平方_________________,并类比阅读材料画图利用所给地砖,画图用图形面积给予几何直观的解释.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com