
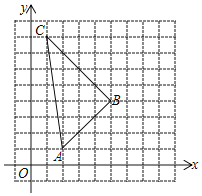
ЁОЬтФПЁПШчЭМЃЌдкЯТСа10ЁС10ЕФЭјИёжаЃЌКсЁЂзнзјБъОљЮЊећЕуЕФЪ§НазіИёЕуЃЌР§ШчAЃЈ2ЃЌ1ЃЉЁЂBЃЈ5ЃЌ4ЃЉЁЂCЃЈ1ЃЌ8ЃЉЖМЪЧИёЕуЃЎ
ЃЈ1ЃЉжБНгаДГіЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉНЋЁїABCШЦЕуBФцЪБеыа§зЊ90ЁуЕУЕНЁїA1BC1ЃЌдкЭјИёжаЛГіЁїA1BC1ЃЛ
ЃЈ3ЃЉдкЭМжаЛГіЯпЖЮEFЃЌЪЙЫќЭЌЪБТњзувдЯТЬѕМўЃКЂйЕуEдкЁїABCФкЃЛЂкЕуEЃЌFЖМЪЧИёЕуЃЛЂлEFШ§ЕШЗжBCЃЛЂмEFЃН![]() ЃЎЧыаДГіЕуEЃЌFЕФзјБъЃЎ
ЃЎЧыаДГіЕуEЃЌFЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ12;ЃЈ2ЃЉМћНтЮі;ЃЈ3ЃЉEЃЈ2ЃЌ4ЃЉЃЌFЃЈ7ЃЌ8ЃЉ.
ЁОНтЮіЁП
ЃЈ1ЃЉгУвЛИіОиаЮЕФУцЛ§ЗжБ№МѕШЅШ§ИіжБНЧШ§НЧаЮЕФУцЛ§ШЅМЦЫуЁїABCЕФУцЛ§ЃЛ
ЃЈ2ЃЉРћгУЭјИёЬиЕуКЭа§зЊЕФаджЪЛГіAЁЂCЕФЖдгІЕуA1ЁЂC1МДПЩЕУЕНЁїA1BC1ЃЛ
ЃЈ3ЃЉРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЕУЕНCFЃКBE=2ЃЌдђEFШ§ЕШЗжBCЃЌШЛКѓаДГіEЁЂFЕФзјБъЃЌИљОнЙДЙЩЖЈРэЧѓГіEFЕФГЄЖШЮЊ![]()
НтЃКЃЈ1ЃЉЁїABCЕФУцЛ§ЃН4ЁС7Љ![]() ЁС7ЁС1Љ
ЁС7ЁС1Љ![]() ЁС3ЁС3Љ
ЁС3ЁС3Љ![]() ЁС4ЁС4ЃН12ЃЛ
ЁС4ЁС4ЃН12ЃЛ
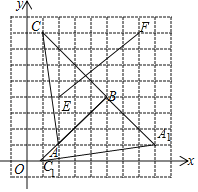
ЃЈ2ЃЉШчЭМЃЌЁїA1BC1ЮЊЫљзїЃЛ
ЃЈ3ЃЉШчЭМЃЌЯпЖЮEFЮЊЫљзїЃЌЦфжаEЕузјБъЮЊЃЈ2ЃЌ4ЃЉЃЌFЕузјБъЮЊЃЈ7ЃЌ8ЃЉЃЌEFЕФГЄЖШЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() АДФцЪБеыЗНЯђа§зЊ
АДФцЪБеыЗНЯђа§зЊ![]() ЕНЯпЖЮ
ЕНЯпЖЮ![]() .
.![]() гЩ
гЩ![]() би
би![]() ЗНЯђЦНвЦЕУЕНЃЌЧвжБЯп
ЗНЯђЦНвЦЕУЕНЃЌЧвжБЯп![]() Й§Еу
Й§Еу![]() .
.
ЃЈ1ЃЉЧѓ![]() ЕФДѓаЁЃЛ
ЕФДѓаЁЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФГЄ.
ЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛСОЕЅГЕЗХдкЫЎЦНЕФЕиУцЩЯЃЌГЕАбЭЗЯТЗН![]() ДІгызјЕцЯТЗН
ДІгызјЕцЯТЗН![]() ДІдкЦНаагкЕиУцЕФЭЌвЛЫЎЦНЯпЩЯЃЌ
ДІдкЦНаагкЕиУцЕФЭЌвЛЫЎЦНЯпЩЯЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФОрРыдМЮЊ
жЎМфЕФОрРыдМЮЊ![]() ЃЌЯжВтЕУ
ЃЌЯжВтЕУ![]() ЃЌ
ЃЌ![]() гы
гы![]() ЕФМаНЧЗжБ№ЮЊ
ЕФМаНЧЗжБ№ЮЊ![]() гы
гы![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕНЕиУцЕФОрРы
ЕНЕиУцЕФОрРы![]() ЮЊ
ЮЊ![]() ЃЌзјЕцжажс
ЃЌзјЕцжажс![]() ДІгыЕу
ДІгыЕу![]() ЕФОрРы
ЕФОрРы![]() ЮЊ
ЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕНЕиУцЕФОрРыЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ.ЃЈВЮПМЪ§ОнЃК
ЕНЕиУцЕФОрРыЃЈНсЙћБЃСєвЛЮЛаЁЪ§ЃЉ.ЃЈВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+cЃЈaЁй0ЃЉОЙ§CЃЈ2ЃЌ0ЃЉЃЌDЃЈ0ЃЌЉ1ЃЉСНЕуЃЌВЂгыжБЯпy=kxНЛгкAЁЂBСНЕуЃЌжБЯпlЙ§ЕуEЃЈ0ЃЌЉ2ЃЉЧвЦНаагкxжсЃЌЙ§AЁЂBСНЕуЗжБ№зїжБЯпlЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуMЁЂNЃЎ

ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжЄЃКAO=AMЃЛ
ЃЈ3ЃЉЬНОПЃК
ЂйЕБk=0ЪБЃЌжБЯпy=kxгыxжсжиКЯЃЌЧѓГіДЫЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЪдЫЕУїЮоТлkШЁКЮжЕЃЌ![]() ЕФжЕЖМЕШгкЭЌвЛИіГЃЪ§ЃЎ
ЕФжЕЖМЕШгкЭЌвЛИіГЃЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЃЈЮЪЬтЗЂЯжЃЉ
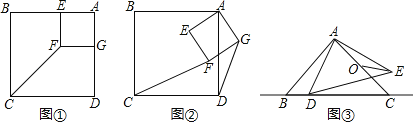
ШчЭМЂйЃЌе§ЗНаЮAEFGЕФСНБпЗжБ№дке§ЗНаЮABCDЕФБпABКЭADЩЯЃЌСЌНгCFЃЎ
ЬюПеЃКЂйЯпЖЮCFгыDGЕФЪ§СПЙиЯЕЮЊЁЁ ЁЁЃЛ
ЂкжБЯпCFгыDGЫљМаШёНЧЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉЃЈЭиеЙЬНОПЃЉ
ШчЭМЂкЃЌНЋе§ЗНаЮAEFGШЦЕуAФцЪБеыа§зЊЃЌдка§зЊЕФЙ§ГЬжаЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃЌЧыРћгУЭМЂкНјааЫЕУїЃЎ
ЃЈ3ЃЈНтОіЮЪЬтЃЉ
ШчЭМЂлЃЌЁїABCКЭЁїADEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃНЁЯDAEЃН90ЁуЃЌABЃНACЃН4ЃЌOЮЊACЕФжаЕуЃЎШєЕуDдкжБЯпBCЩЯдЫЖЏЃЌСЌНгOEЃЌдђдкЕуDЕФдЫЖЏЙ§ГЬжаЃЌЯпЖЮOEГЄЕФзюаЁжЕЮЊЁЁ ЁЁЃЈжБНгаДГіНсЙћЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
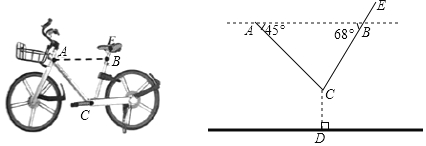
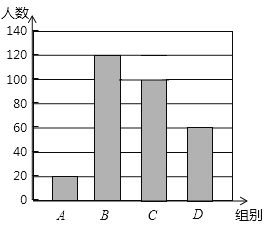
ЁОЬтФПЁПЙњМвЙцЖЈЃЌжаЁЂаЁбЇЩњУПЬьдкаЃЬхг§ЛюЖЏЪБМфВЛЕЭгк1hЃЎЮЊДЫЃЌФГЧјОЭЁАФуУПЬьдкаЃЬхг§ЛюЖЏЪБМфЪЧЖрЩйЁБЕФЮЪЬтЫцЛњЕїВщСЫЯНЧјФк300УћГѕжабЇЩњЃЎИљОнЕїВщНсЙћЛцжЦГЩЕФЭГМЦЭМШчЭМЫљЪОЃЌЦфжаAзщЮЊtЃМ0.5hЃЌBзщЮЊ0.5hЁмtЃМ1hЃЌCзщЮЊ1hЁмtЃМ1.5hЃЌDзщЮЊtЁн1.5hЃЎ
ЧыИљОнЩЯЪіаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЕїВщЪ§ОнЕФжкЪ§Тфдк зщФкЃЌжаЮЛЪ§Тфдк зщФкЃЛ
ЃЈ2ЃЉИУЯНЧјдМга18000УћГѕжабЇЩњЃЌЧыФуЙРМЦЦфжаДяЕНЙњМвЙцЖЈЬхг§ЛюЖЏЪБМфЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
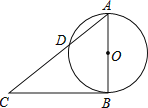
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЕуCЪЧЁбOЭтЕФвЛЕуЃЌCBгыЁбOЯрЧагкЕуBЃЌACНЛЁбOгкЕуDЃЌЕуEЪЧ![]() ЩЯЕФвЛЕуЃЈВЛгыЕуAЃЌBЃЌDжиКЯЃЉЃЌШєЁЯCЃН48ЁуЃЌдђЁЯAEDЕФЖШЪ§ЮЊ_____ЃЎ
ЩЯЕФвЛЕуЃЈВЛгыЕуAЃЌBЃЌDжиКЯЃЉЃЌШєЁЯCЃН48ЁуЃЌдђЁЯAEDЕФЖШЪ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
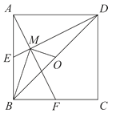
ЁОЬтФПЁПШчЭМЃЌвбжЊEЃЌFЗжБ№ЮЊе§ЗНаЮABCDЕФБпABЃЌBCЕФжаЕуЃЌAFгыDEНЛгкЕуMЃЌOЮЊBDЕФжаЕуЃЌдђЯТСаНсТлЃКЂйЁЯAME=90ЁуЃЛЂкЁЯBAF=ЁЯEDBЃЛЂлЁЯBMO=90ЁуЃЛЂмMD=2AM=4EMЃЛЂн![]() ЃЎЦфжае§ШЗНсТлЕФЪЧЃЈ ЃЉ
ЃЎЦфжае§ШЗНсТлЕФЪЧЃЈ ЃЉ
A. ЂйЂлЂмB. ЂкЂмЂнC. ЂйЂлЂнD. ЂйЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
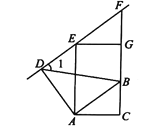
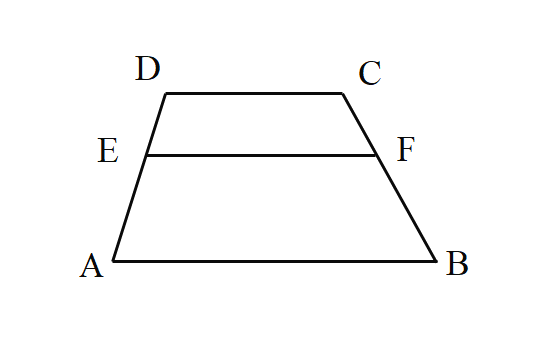
ЁОЬтФПЁПШчЭМЃЌвбжЊдкЬнаЮABCDжаЃЌAB//CDЃЌAB=12ЃЌCD=7ЃЌЕуEдкБпADЩЯЃЌ![]() ЃЌЙ§ЕуEзїEF//ABНЛБпBCгкЕуF.
ЃЌЙ§ЕуEзїEF//ABНЛБпBCгкЕуF.
ЃЈ1ЃЉЧѓЯпЖЮEFЕФГЄЃЛ
ЃЈ2ЃЉЩш![]() ЃЌ
ЃЌ![]() ЃЌСЊНсAFЃЌЧыгУЯђСП
ЃЌСЊНсAFЃЌЧыгУЯђСП![]() БэЪОЯђСП
БэЪОЯђСП![]() .
.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com