【题目】计算
（1）33.1﹣10.7﹣（﹣229）﹣|﹣
|
（2）
（3）（﹣36）×
（4）4﹣（﹣2）
（5）﹣3﹣[﹣5+（1﹣2×
）÷（﹣2）]
（6）（﹣96）×（﹣0.125）+96×
+（﹣96）×
（7）﹣14+（﹣3）×[（﹣4）2+2]﹣（﹣2）3÷4
【答案】（1）249.1；（2）﹣
；（3）-30；（4）-14；（5）1.9；（6）-96；（7）-53.
【解析】
(1)先去括号和绝对值，然后把分数化为小数，最后再根据有理数的加减法进行计算，即可得到正确答案；
(2)把分数化为假分数，然后进行运算.同级运算从左到右计算，除以一个数等于乘以这个数的倒数；
(3)先利用乘法分配律计算，再计算加减即可；
(4)要注意运算顺序与运算符号，本题应先做乘除法，再进行加减运算；
(5)按照有理数混合运算的顺序，先乘除算加减，有括号的先算括号里面的；
(6) 原式逆用乘法分配律进行计算即可；
(7) 根据有理数混合运算的法则先算括号里面的，再算乘方，乘除，最后算加减即可．
解：（1）33.1﹣10.7﹣（﹣229）﹣|﹣
|
＝33.1﹣10.7+229﹣2.3
＝（33.1+229）﹣（10.7+2.3）
＝262.1﹣13
＝249.1；
（2）
（3）
＝﹣36×
﹣36×
﹣36×（﹣
）+5
＝﹣20﹣42+27+5
＝﹣62+32
＝﹣30；
（4）
＝4+6×（﹣3）
＝4﹣18
＝﹣14；
（5）﹣3﹣[﹣5+（1﹣2×
）÷（﹣2）]
＝﹣3﹣[﹣5+（1﹣1.2）÷（﹣2）]
＝﹣3﹣[﹣5+（﹣0.2）÷（﹣2）]
＝﹣3﹣（﹣5+0.1）
＝﹣3+4.9
＝1.9；
（6）（﹣96）×（﹣0.125）+96×
+（﹣96）×
＝96×（0.125+﹣）
＝96×（﹣1）
＝﹣96；
（7）﹣14+（﹣3）×[（﹣4）2+2]﹣（﹣2）3÷4
＝﹣1+（﹣3）×（16+2）﹣（﹣8）÷4
＝﹣1+（﹣3）×18+2
＝﹣1﹣54+2
＝﹣53；
科目：初中数学 来源： 题型：
【题目】(1)根据下面给出的数轴，解答下面的问题：
①请你根据图中A、B两点的位置，分别写出它们所表示的有理数A：______，B：______；
②观察数轴，与点A的距离为4的点表示的数是：______；
③若将数轴折叠，使得A点与-3表示的点重合，则B点与数______表示的点重合．
(2)如图，数轴上A，B两点对应的有理数分别为10和15，点P从点A出发，以每秒1个单位长度的速度沿数轴正方向运动，点Q同时从原点O出发，以每秒2个单位长度的速度沿数轴正方向运动，设运动时间为t秒．
①当0＜t＜5，用含t的式子填空：BP＝______，AQ＝______；
②当t＝2时，求PQ的值；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察算式：
；
；
；
按规律填空
（1）
+
+
+
=______；
（2）++++…+
=________；
（3）如果n为正整数，那么
++++…+
=______；
（4）由此拓展写出具体过程:
+
+
+…+
=______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，点D是边BC的中点，点E在△ABC内，AE平分∠BAC，CE⊥AE，点F在边AB上，EF∥BC．
（1）求证：四边形BDEF是平行四边形；
（2）线段BF、AB、AC的数量之间具有怎样的关系？证明你所得到的结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某自行车厂一周内计划平均每天生产200辆自行车，由于种种原因，实际每天生产量与计划量相比有出入．下表是某周的生产情况（超产记为正，减产记为负）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减产量/辆 |
|
|
|
|
|
|
|
（1）根据记录的数据可知，该厂星期五生产自行车 辆．
（2）根据上表记录的数据可知，该厂本周实际生产自行车 辆．
（3）该厂实行每日计件工资制，每生产一辆自行车可得60元，若超额完成任务，则超过部分每辆另外奖励15元，若完不成每天的计划量，则少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
（4）若该厂实行每周计件工资制，每生产一辆自行车可得60元，若超额完成周计划工作量，则超过部分每辆另外奖励15元，若完不成每周的计划量，则少生产一辆扣20元，那么该厂工人这一周的工资总额是多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
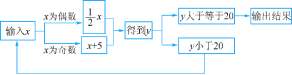
【题目】按如图所示的程序计算，若输入的值x＝17，则输出的结果为22；若输入的值x＝34，则输出的结果为22.当输出的值为24时，则输入的x的值在0至40之间的所有正整数是____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．
（1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）
（2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？
（3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，DE//BC，∠ADE=∠EFC,将说明∠1=∠2成立的理由填写完。
解:
DE//BC （ ）
∠ADE=_________ （ ）
∠ADE=∠EFC （ ）
_____________=_____________ （ ）
DB//EF（ ）
∠1= ∠2 （ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
