
【题目】我们定义:如图1,在△ABC看,把AB点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
【答案】(1)①![]() ;②4;(2) AD=
;②4;(2) AD=![]() BC.
BC.
【解析】试题分析:(1)①首先证明△ADB′是含有30°是直角三角形,可得AD=![]() AB′即可解决问题;②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
AB′即可解决问题;②首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)如图1中,延长AD到Q,使得AD=DQ,连接B′Q,C′Q,根据∠QB′A=∠BAC,QB′=AC′=AC,AB′=AB,即可得到△AQB′≌△BAC,即可解决问题.
试题解析:
解:(1)①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD=![]() BC;
BC;
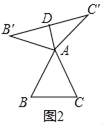
理由:∵△ABC是等边三角形,
∴AB=BC=AC=AB′=AC′,
∵DB′=DC′,
∴AD⊥B′C′,
∵∠BAC=60°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=120°,
∴∠B′=∠C′=30°,
∴AD=![]() AB′=
AB′=![]() BC,
BC,
故答案为![]() .
.
②如图3,当∠BAC=90°,BC=8时,则AD长为4.
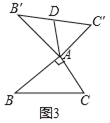
理由:∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD=![]() B′C′=
B′C′=![]() BC=4,
BC=4,
故答案为4.
(2)猜想AD=![]() BC.
BC.
证明:如图,延长AD至点Q,则△DQB'≌△DAC',
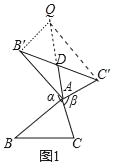
∴QB'=AC',QB'∥AC',
∴∠QB'A+∠B'AC'=180°,
∵∠BAC+∠B'AC'=180°,
∴∠QB'A=∠BAC,
又由题意得到QB'=AC'=AC,AB'=AB,
∴△AQB'≌△BCA,
∴AQ=BC=2AD,
即AD=![]() BC.
BC.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
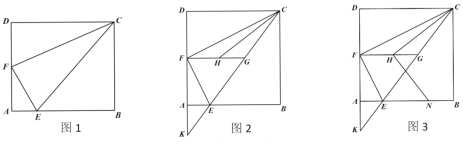
【题目】已知:在矩形ABCD中,点F为AD中点,点E为AB边上一点,连接CE、EF、CF,EF平分∠AEC.
(1)如图1,求证:CF⊥EF;
(2)如图2,延长CE、DA交于点K, 过点F作FG∥AB交CE于点G若,点H为FG上一点,连接CH,若∠CHG=∠BCE, 求证:CH=FK;
(3)如图3, 过点H作HN⊥CH交AB于点N,若EN=11,FH-GH=1,求GK长.
查看答案和解析>>
科目:初中数学 来源: 题型:
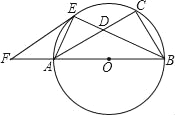
【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AB=2,以点A为圆心,AB为半径的圆交边BC于点E,连接DE、AC、AE.
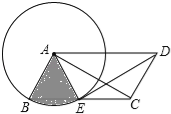
(1)求证:△AED≌△DCA;
(2)若DE平分∠ADC且与⊙A相切于点E,求图中阴影部分(扇形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,且
,且![]() .
.
![]()
![]() 则
则![]() ________,
________,![]() ________;并将这两个数在数轴上所对应的点
________;并将这两个数在数轴上所对应的点![]() ,
,![]() 表示出来;
表示出来;
![]() 数轴上在
数轴上在![]() 点右边有一点
点右边有一点![]() 到
到![]() 、
、![]() 两点的距离和为
两点的距离和为![]() ,若点
,若点![]() 的数轴上所对应的数为
的数轴上所对应的数为![]() ,求
,求![]() 的值;
的值;
![]() 若点
若点![]() ,点
,点![]() 同时沿数轴向正方向运动,点
同时沿数轴向正方向运动,点![]() 运动的速度为
运动的速度为![]() 单位/秒,点
单位/秒,点![]() 运动的速度为
运动的速度为![]() 单位/秒,若
单位/秒,若![]() ,求运动时间
,求运动时间![]() 的值.
的值.
(温馨提示:![]() 、
、![]() 之间距离记作
之间距离记作![]() ,点
,点![]() 、
、![]() 在数轴上对应的数分别为
在数轴上对应的数分别为![]() 、
、![]() ,则
,则![]() .)
.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
(a<0)图象与x轴的交点A、B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
①16a﹣4b+c<0;②若P(﹣5,y1),Q(![]() ,y2)是函数图象上的两点,则y1>y2;③a=﹣
,y2)是函数图象上的两点,则y1>y2;③a=﹣![]() c;④若△ABC是等腰三角形,则b=﹣
c;④若△ABC是等腰三角形,则b=﹣![]() .其中正确的有______(请将结论正确的序号全部填上)
.其中正确的有______(请将结论正确的序号全部填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,AB=AC.D,E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB,连接EF,下列结论:
①△AED≌△AEF;
②△ABE∽△ACD;
③BE+DC=DE;
④BE2+DC2=DE2.
其中正确的是( )

A.②④ B.①④ C.②③ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示:
![]()
(1)比较大小:b____0, a____c, b____c, b-a____0;
(2)A,B两点间的距离为__________,B,C两点间的距离为_______;
(3)化简:|b|-|b+c|+|c-a|-|a+c|-|b-c|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用四个长为m,宽为n的相同长方形按如图方式拼成一个正方形.
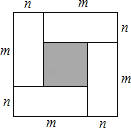
(1)根据图形写出一个代数恒等式: ;
(2)已知3m+n=9,mn=6,试求3m﹣n的值;
(3)若m+n=1,求m2+n2的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com