
����Ŀ���Ķ���һ��أ�һ����Ԫһ�η���ax��by��c (a��b��cΪ��������a��b����Ϊ0)��������⣬���ǹ涨������ÿһ������x��y��ֵ�ֱ���Ϊһ����ĺᡢ�����������ƽ��ֱ������ϵ�У��������Ǿ͵õ��˶�Ԫһ�η��̵�ͼ��һ��ֱ�ߡ�����Ԫһ�η��̵Ľ���������Ӧֱ���ϵ�����꣺��ֱ֮���ϵ�������Ϊ���Ӧ�Ķ�Ԫһ�η��̵Ľ⡣��2x ��y = 0����һ��x��1��y��2���Ӧ��ͼ����һ�㣨1,2��.
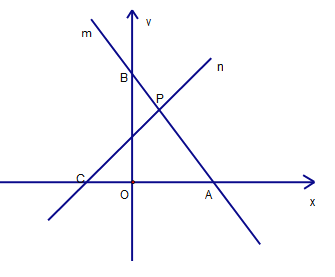
��1����ͼ��4x��3y��12��ͼ��Ϊֱ��m������x�ύ��A������Ϊ ���� �� y�ύ��B������Ϊ ��
��2��ͼ��ax��by����5��ͼ��Ϊֱ��n������x�ύ��C��![]() ��0�����루1����ֱ��m����P������P�ĺ�����Ϊ1 ����a��b��ֵ.
��0�����루1����ֱ��m����P������P�ĺ�����Ϊ1 ����a��b��ֵ.
 �¿α�ͬ��ѵ��ϵ�д�
�¿α�ͬ��ѵ��ϵ�д� һ����ʦ����Ӧ����������һ��ȫϵ�д�
һ����ʦ����Ӧ����������һ��ȫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У��Խ���AC��BD���ڵ�E����BAC=90�㣬��CED=45�㣬��DCE=30�㣬DE=![]() ��BE=
��BE=![]() ����CD�ij����ı���ABCD�������
����CD�ij����ı���ABCD�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
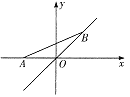
����Ŀ����ͼ����A������Ϊ��-1��0������B��ֱ��![]() ���˶������߶�AB���ʱ����B������Ϊ�� ��
���˶������߶�AB���ʱ����B������Ϊ�� ��
A. ��0��0�� B. ��![]() ��
��![]() �� C. ��
�� C. ��![]() ��
��![]() �� D. ��
�� D. ��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒ��˾��ij������һ��ţ�̣�����·����ÿǧ�����˷�0.60Ԫ���ɹ�·���䣬ÿǧ�����˷�0.30Ԫ�����貹��600Ԫ
��1����ù�˾���������ţ��Ϊxǧ�ˣ�ѡ����·����ʱ�������˷�Ϊy1Ԫ��ѡ��·����ʱ�������˷�Ϊy2Ԫ����ֱ�д��y1��y2��x֮��Ĺ�ϵʽ��
��2������˾ֻ֧���˷�1500Ԫ����ѡ���������䷽ʽ���͵�ţ�̶ࣿ����˾����1500ǧ��ţ�̣���ѡ���������䷽ʽ������ý��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E��F�ǶԽ���BD�ϵ����㣬��BE=DF��
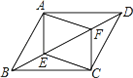
��1����֤���ı���AECF��ƽ���ı��Σ�
��2������ı���ABCD�����Σ���֤���ı���AECFҲ�����Σ�
��3������ı���ABCD�Ǿ��Σ����ж��ı���AECF����״������д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10�֣�ij�̳���2500Ԫ������A��B�������ͽ���̨�ƹ�50յ��������̨�ƵĽ��ۣ�������±���ʾ��
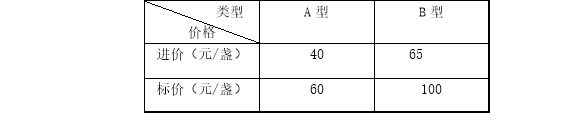
��1��������̨�Ƹ���������յ��
��2����A��̨�ư���۵ľ��۳��ۣ�B��̨�ư���۵İ��۳��ۣ���ô����̨��ȫ��������̳�����������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������ϣ���![]() �ij�ʼλ�ñ�ʾ����Ϊ
�ij�ʼλ�ñ�ʾ����Ϊ![]() ���ֵ�
���ֵ�![]() �������ƶ�����1�ε�
�������ƶ�����1�ε�![]() �����ƶ�3����λ��������
�����ƶ�3����λ��������![]() ����2�δӵ�
����2�δӵ�![]() �����ƶ�6����λ��������
�����ƶ�6����λ��������![]() ����
����![]() �δӵ�
�δӵ�![]() �����ƶ�
�����ƶ�![]() ����λ��������
����λ��������![]() ���������������ƶ���ʽ�������ƣ������
���������������ƶ���ʽ�������ƣ������![]() ��ԭ��ľ��벻С��
��ԭ��ľ��벻С��![]() ����ô
����ô![]() ����Сֵ��___��
����Сֵ��___��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�DZ߳�Ϊ3�ĵȱ������Σ���D�DZ�BC�ϵ�һ�㣬��BD��1����ADΪ�����ȱߡ�ADE������E��EF��BC����AC�ڵ�F������BF�������н���������ABD�ա�BCF�����ı���BDEF��ƽ���ı��Σ���S�ı���BDEF��![]() ����S��AEF��
����S��AEF��![]() ��������ȷ����(����)
��������ȷ����(����)

A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BA=BC=20cm��AC=30cm����P��A��������AB��4cm/s���ٶ����B�˶���ͬʱ��Q��C���������CA��3cm/s���ٶ���A���˶������˶�ʱ��Ϊx��s����

��1����xΪ��ֵʱ��PQ��BC��
��2������APQ����CQB����ʱ��AP�ij�Ϊ________����
��3����S��BCQ��S��ABC=1��3����S��APQ��S��ABQ��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com