练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

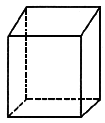
    如图，在正方体中我们可以截出三角形、四边形、五边形和六边形，请你尝试一下，能够截出七边形吗？若能，画出截面图，若不能，说明理由．

    答案：
    解析：

    可以截出三角形、四边形、五边形、六边形．不能截出七边形，因为和正方体的棱最多只能有6个不同的交点(图略)


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    24、如图①，一个无盖的正方体盒子的棱长为10厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙．（盒壁的厚度忽略不计）
    （1）假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连接AE、EC1．虫乙如果沿路径A-E-C1爬行，那么可以在最短的时间内捕捉到昆虫甲．仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲；（请简要说明画法）
    （2）如图②，假设昆虫甲从顶点C1，以1厘米/秒的速度在盒子的内部沿棱C1C向下爬行，同时昆虫乙从顶点A以2厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？（精确到1秒）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

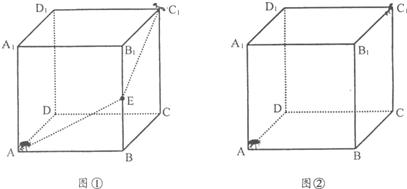
    (10分) 如图①，一个无盖的正方体盒子的棱长为6厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙．（盒壁的厚度忽略不计）

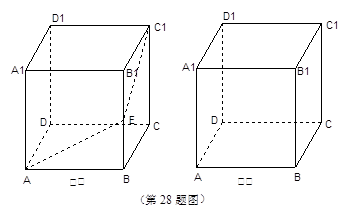
    （1）假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连结 AE、EC1．昆虫乙如果沿路径 A → E → Cl 爬行 , 那么可以在最短的时间内捕捉到昆虫甲．仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲．（请简要说明画法）

    （2）如图②，假设昆虫甲从顶点C1以1厘米/秒的速度沿盒子的棱C1D1向D1爬行，同时昆虫乙从顶点A以2.5厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    (10分) 如图①，一个无盖的正方体盒子的棱长为6厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙．（盒壁的厚度忽略不计）

    （1）假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连结AE、EC1．昆虫乙如果沿路径A→E→Cl 爬行 , 那么可以在最短的时间内捕捉到昆虫甲．仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲．（请简要说明画法）
    （2）如图②，假设昆虫甲从顶点C1以1厘米/秒的速度沿盒子的棱C1D1向D1爬行，同时昆虫乙从顶点A以2.5厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？

    查看答案和解析>>

    科目：初中数学 来源：2010年辽宁省大连市初二数学阶段性检测数学卷 题型：解答题

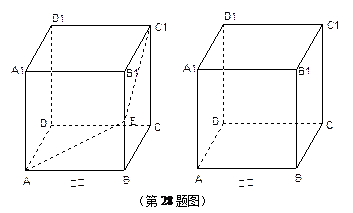
    (10分) 如图①，一个无盖的正方体盒子的棱长为6厘米，顶点C1处有一只昆虫甲，在盒子的内部顶点A处有一只昆虫乙．（盒壁的厚度忽略不计）

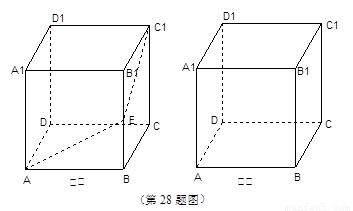
    （1）假设昆虫甲在顶点C1处静止不动，如图①，在盒子的内部我们先取棱BB1的中点E，再连结 AE、EC1．昆虫乙如果沿路径 A → E → Cl 爬行 , 那么可以在最短的时间内捕捉到昆虫甲．仔细体会其中的道理，并在图①中画出另一条路径，使昆虫乙从顶点A沿这条路径爬行，同样可以在最短的时间内捕捉到昆虫甲．（请简要说明画法）

    （2）如图②，假设昆虫甲从顶点C1以1厘米/秒的速度沿盒子的棱C1D1向D1爬行，同时昆虫乙从顶点A以2.5厘米/秒的速度在盒壁上爬行，那么昆虫乙至少需要多长时间才能捕捉到昆虫甲？

     

    查看答案和解析>>

    同步练习册答案