练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．抛物线y=ax2+ax-2过直线y=mx-2m+2上的定点A，求抛物线的解析式．

    分析 先求出定点A，再代入抛物线解析式即可解决．

    解答 解：∵直线y=mx-2m+2上的定点A，
    ∴点A坐标（2，2），
    把A（2，2）代入抛物线y=ax2+ax-2得，2=4a+2a-2，
    ∴a=$\frac{2}{3}$，
    ∴抛物线解析式为y=$\frac{2}{3}$x2+$\frac{2}{3}$x-2．

    点评 本题考查待定系数法确定二次函数解析式，解题的关键是确定定点A的坐标，熟练掌握待定系数法，属于中考常考题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    5．设a≠b，m≠n，a，b，m，n是已知数，则方程组$\left\{\begin{array}{l}\frac{x}{a+m}+\frac{y}{b+m}=1\\ \frac{x}{a+n}+\frac{y}{b+n}=1\end{array}\right.$的解是（　　）
    A．$\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a+b}\\ y=\frac{（b+m）（b+n）}{a+b}\end{array}\right.$B．$\left\{\begin{array}{l}x=\frac{（a+m）（b+m）}{a-b}\\ y=\frac{（a+n）（b+n）}{a-b}\end{array}\right.$
    C．$\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a-b}\\ y=\frac{（b+m）（b+n）}{a-b}\end{array}\right.$D．$\left\{\begin{array}{l}x=\frac{（a+m）（a+n）}{a-b}\\ y=-\frac{（b+m）（b+n）}{a-b}\end{array}\right.$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．反比例函数y=（2m-1）${x}^{{m}^{2}-1}$，当x＞0时，y随x的增大而增大，则m的值是（　　）
    A．±1B．小于$\frac{1}{2}$的实数C．-1D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图，已知⊙O的半径OA⊥OB，过点A的直线交OB于点P，交⊙O于点Q，过Q点引⊙O的切线交OB的延长线于点C，求证：CP=CQ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．将正整数1，2，3，4…按以下方式排列
     
    根据排列规律，从2015到2017的箭头依次为（　　）
    A．↓→B．→↓C．↑→D．→↑

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

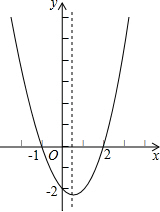    20．二次函数y=ax2+bx+c（a≠0）的大致图象如图，关于该二次函数，下列说法错误的是（　　）
    A．函数有最小值B．对称轴是直线x=$\frac{1}{2}$
    C．当x＜$\frac{1}{2}$时，y随x的增大而减小D．当-1＜x＜3时，y＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列计算正确的是（　　）
    A．a3÷a=a3B．a+a=2aC．（a3）2=a9D．a2•a2=2a2

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．下列各组数中，互为相反数的一组是（　　）
    A．-2与$\sqrt{（-2）^{2}}$B．-2与$\root{3}{-8}$C．2与$\sqrt{-4}$D．$\sqrt{1{0}^{-4}}$与2

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

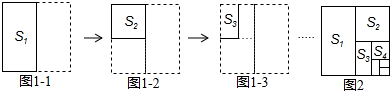
    5．将边长为1的正方形纸片按图1所示方法进行对折，记第1次对折后得到的图形面积为S1，第2次对折后得到的图形面积为S2，…，第n次对折后得到的图形面积为Sn，请根据图2化简，S1+S2+S3+…+S2016=1-$\frac{1}{{2}^{2016}}$．

    查看答案和解析>>

    同步练习册答案