
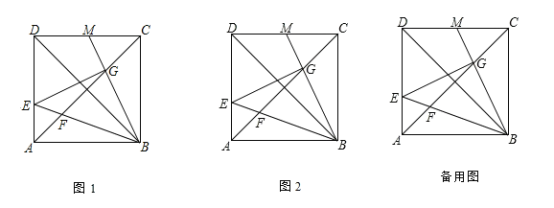
【题目】如图,在边长为6的正方形ABCD中,点E为AD边上的一个动点(与点A、D不重合),∠EBM=45°,BE交对角线AC于点F,BM交对角线AC于点G、交CD于点M.
(1)如图1,联结BD,求证:![]() ,并写出
,并写出![]() 的值;
的值;
(2)联结EG,如图2,若设![]() ,求y关于
,求y关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当M为边DC的三等分点时,求![]() 的面积.
的面积.
【答案】![]() ;
;![]() ;
;![]() 或
或![]()
【解析】
(1)根据正方形的性质得到∠EDB=∠GCB=45°,∠ABD=∠CBD=45°,根据相似三角形的判定定理证明即可;
(2)作EH⊥AC于H,根据等腰直角三角形的性质、勾股定理和相似三角形的性质得到y关于x的函数解析式;
(3)分CM=![]() CD和CM=
CD和CM=![]() CD两种情况,根据相似三角形的性质解答即可.
CD两种情况,根据相似三角形的性质解答即可.
(1)证明:∵四边形ABCD是正方形,
∴∠EDB=∠GCB=45°,∠ABD=∠CBD=45°,又∠EBM=45°,
∴∠GBC+∠DBM=45°,∠EBD+∠DBM=45°,
∴∠GBC=∠EBD,又∠EDB=∠GCB=45°,
∴△DEB∽△CGB,
∴DE:CG=BD:BC=![]() ;
;
(2)如图2,作EH⊥AC于H,
则AH=EH=![]() x,
x,
∵△DEB∽△CGB,
∴![]() ,
,
∴CG=![]() (6x),
(6x),
∴HG=ACAHCG=3![]() ,
,
∵EG2=EH2+HG2,
∴![]() ;
;
(3)当CM=![]() CD=2时,
CD=2时,
∵四边形ABCD是正方形,
∴CD∥AB,
∴![]() ,
,
∴CG=![]() ,
,
∴DE=3,则AE=3,
∴AH=EH=![]() ,
,
∵AD∥BC,
∴![]() ,
,
∴AF=2![]() ,
,
∴GF=ACAFCG=![]() ,
,
∴S△EGF=![]() ×FG×EH=
×FG×EH=![]() ,
,
当CM=![]() CD=4时,
CD=4时,![]() ,
,
∴CG=![]() ,
,
∴DE=![]() ,则AE=
,则AE=![]() ,
,
AH=EH=![]() ,
,
∵![]() ,
,
∴AF=![]() ,
,
∴GF=ACAFCG=![]() ,
,
∴S△EGF=![]() ×FG×EH=
×FG×EH=![]() .
.
综上,S△EGF=![]() 或
或![]()


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
(1)求抛物线的解析式;
(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.
(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备租用一批汽车,现有甲、乙两种大客车,甲种客车每辆载客量45人,乙种客车每辆载客量30人,已知1辆甲种客车和3辆乙种客车共需租金1240元,3辆甲种客车和2辆乙种客车共需租金1760元.
(1)求1辆甲种客车和1辆乙种客车的租金分别是多少元?
(2)学校计划租用甲、乙两种客车共8辆,送330名师生集体外出活动,最节省的租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,若点
中,若点![]() 和点
和点![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,则称点
对称,则称点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点.
的二次对称点.
(1)如图1,点![]() .
.
①若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则点
的二次对称点,则点![]() 的坐标为________;
的坐标为________;
②若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,则
的二次对称点,则![]() 的值为_______;
的值为_______;
③若点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() 的二次对称点,则直线
的二次对称点,则直线![]() 的表达式为__________;
的表达式为__________;
(2)如图2,![]() 的半径为1.若
的半径为1.若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直绩
轴,直绩![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在射线
在射线![]() 上,
上,![]() 的取值范围是________;
的取值范围是________;
(3)![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 的半径为2,若
的半径为2,若![]() 上存在点
上存在点![]() ,使得点
,使得点![]() 是点
是点![]() 关于
关于![]() 轴,直线
轴,直线![]() :
:![]() 的二次对称点,且点
的二次对称点,且点![]() 在
在![]() 轴上,求
轴上,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=2,E是AB的中点,直线![]() 平行于直线EC,且直线
平行于直线EC,且直线![]() 与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线
与直线EC之间的距离为2,点F在矩形ABCD边上,将矩形ABCD沿直线EF折叠,使点A恰好落在直线![]() 上, 则DF的长为_____
上, 则DF的长为_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB的长为65米,坡度i=1∶2.4,BC⊥AC.
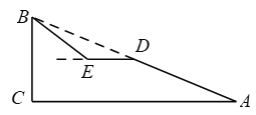
(参考三角函数:sin37°≈ ![]() ,cos37°≈
,cos37°≈ ![]() ,tan37°≈
,tan37°≈ ![]() )
)
(1)求斜坡的高度BC.
(2)现计划在斜坡AB的中点D处挖去部分坡体,修建一个平行于水平线CA的平台DE和一条新的斜坡BE,若斜坡BE的坡角为37°,求平台DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,依次连接第一个矩形各边的中点得到一个菱形,再依次连接菱形各边的中点得到第二个矩形,按照此方法继续下去.已知第一个矩形的两条邻边长分别为6和8,则第n个菱形的周长为______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com