
科目:初中数学 来源: 题型:解答题
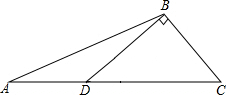 如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)
如图,在钝角△ABC中,过钝角顶点B作BD⊥BC交AC于点D.请用尺规作图法在BC边上求作一点P,使得点P到AC的距离等于BP的长.(保留作图痕迹,不写作法)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 180 | 185 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
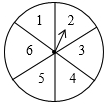 如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.
如图,一个质地均匀的转盘被平均分成6等份,分别标有数字1,2,3,4,5,6,当它停止时,指针指向的数字即为转出的数字(若指针指在分界线上,则重新转动转盘).小颖与小亮进行转盘游戏,规则是:若转出的数是3的倍数则小颖获胜,若不是3的倍数则小亮获胜.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.
如图,已知EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数,下面给出了求∠AGD的度数的过程,将此补充完整并在括号里填写依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年 度 | 2013 | 2014 | 2015 | 2016 |
| 投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
| 产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com