
����Ŀ����ͼ1��E��������ABCD��AB�ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת90����ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
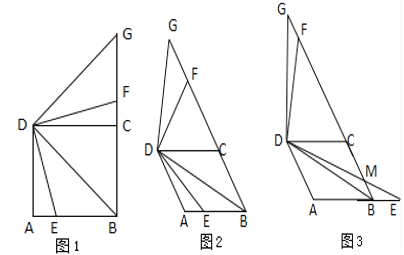
��1��̽���߶�BE��BF��DB֮���������ϵ��д�����۲�����֤����
��2�����ı���ABCDΪ���Σ���ADC=60����E������ABCD��AB����ֱ���ϵ�һ�㣬����BD��DE������BDE�Ƶ�D��ʱ����ת120����ת��ǵ����߷ֱ�������BC���ڵ�F�͵�G��
����ͼ2����E���߶�AB��ʱ����̽���߶�BE��BF��BD֮���������ϵ��д�����۲�����֤����
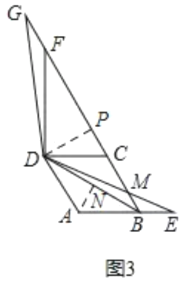
����ͼ3����E���߶�AB���ӳ�����ʱ��DE������BC�ڵ�M����BE=1��AB=2��ֱ��д���߶�GM�ij��ȣ�
���𰸡���1��![]() ��֤������������2����
��֤������������2����![]() ��֤������������
��֤������������![]()
��������
��1��������ת�����ʿ�֤�á�BDG�ǵ���ֱ�������Σ��õ�![]() ����֤����FDG�ա�EDB��ASA�����õ�FG=BE���ɵõ�
����֤����FDG�ա�EDB��ASA�����õ�FG=BE���ɵõ�![]() ��
��
��2���ٸ������ε������Լ���ת�����ʿɵá�DBG=��G=30�����Ӷ�֤����EDB�ա�FDG��ASA�����õ�BF+BE=BF+FG=BG������D��DP��BG�ڵ�P�����ù��ɶ��������������ε����ʵõ�BG=![]() ���Ӷ��ó�
���Ӷ��ó�![]() ���ɣ�
���ɣ�
�ڹ���A��AN��BD��BD�ڵ�N�����ݺ�30��ֱ�������ε����ʼ����������ε����ʣ�����BD��BF�ij�������ƽ���߷��߶γɱ��������ɵ�BM�ij��������߶εIJ�ɵý��ۣ�
�⣺��1��![]() ��
��
���ɣ�����ת��֪����BDE=��FDG����BDG=90����
���ı���ABCD�������Σ�
���CBD=45����
���G=45����
���G=��CBD=45����
��BD=DG��
��BDG�ǵ��������Σ�
��![]() ��
��
���ڡ�FDG���EDB�У�
��FDG=��EDB����G=��DBE=45����BD=DG��
���FDG�ա�EDB��ASA����
��FG=BE
��BE+BF=FG+BF=BG=![]() ��
��
��![]()
��2����![]()
���ɣ���ͼ2��������ABCD�У���ADB=��CDB=![]() ��ADC=30����
��ADC=30����
����ת120����֪����EDF=��BDG=120������EDB=��FDG��
�ڡ�DBG�У���G=180��-120��-30��=30����
���DBG=��G=30����
DB=DG��
���EDB�ա�FDG��ASA����
��BE=FD��
��BF+BE=BF+FG=BG��
����D��DP��BG�ڵ�P��
��BD=DG����BG=2BP��
�ߡ�DBC=30����
��DP=![]() ��
��
����Rt��BDP��![]() ��
��
��BG=![]()
��![]()
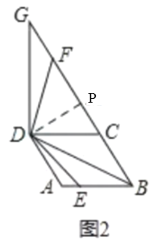
����ͼ3������A��AN��BD��BD�ڵ�N��
��Rt��ABN����ABN=30����AB=2��
��AN=1��BN=![]() ��
��
��BD=2BN=2![]() ��
��
��DC��BE��
��![]() ��
��
��CM+BM=2��
��BM=![]() ��
��
Rt��BDP����DBP=30����BD=2![]() ��
��
��BP=3
����ת�ã�BD=FD��
��BF=2BP=6��
��GM =BG-BM=6+1-![]() =
=![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������ϵ�У���֪��B��8��0�����ȱ�������OAB�Ķ���A�ڷ���������y��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��1�����������ı���ʽ��
��2���ѡ�OAB����ƽ��a����λ���ȣ���Ӧ�õ���O��A��B�������������ͼ����O��A��B��һ�ߵ��е�ʱ����a��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ڼ䣬С���游ĸ��ij����ʤ�زι������������ο�����O����þ���A���䱱ƫ��72�㷽��þ���B������ƫ��40�㷽��С�����ο���������2ǧ���ᄚ��A����֪����B����λ�ھ���A�����Ϸ�����A��B֮��ľ��룮�������ȷ��0.1ǧ�ף�
���ο����ݣ�sin72����0.95��cos72���0.31��sin40���0.64��tan40���0.84��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ʵ��������˳���Ĺ��������������ƻ��Գ�����·�����˸��죬�ְ��żס����������̶���ɣ���֪�ӵĹ���Ч�����Ҷӹ���Ч�ʵ�![]() �����Ӹ���360�ĵ�·���ҶӸ���ͬ�����ĵ�·����3�죮
�����Ӹ���360�ĵ�·���ҶӸ���ͬ�����ĵ�·����3�죮
��1���ס��������̶�ÿ���ܸ����·�ij��ȷֱ��Ƕ����ף�
��2�����ӹ���һ���踶����7��Ԫ���Ҷӹ���һ���踶����5��Ԫ���������ĵ�·ȫ��1200�ף������ܷ��ò�����145��Ԫ�����ٰ��żӹ��������죿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʡ��γ̸ĸ��������̽���ijУ�����ˣ�A������Ӱ��������߶ȣ�B��������������C����������D���������ĶԳ�ͼ�Σ�������ѧʵ����Σ��涨ÿ��ѧ����ѡ��ֻ��ѡ��һ��ʵ����Σ�ѧУ��ѧ��ѡ��ʵ����ε�������г������飬�����������Ƴ�����������������ͳ��ͼ��
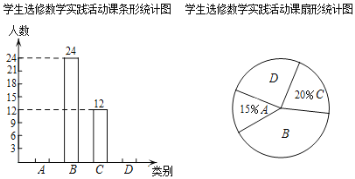
����ͼ����Ϣ����������⣺
��1�����ι�����______��ѧ��������ͳ��ͼ��B����Ӧ�����ε�Բ�Ľ�Ϊ______�ȣ�
��2����ȫ����ͳ��ͼ��
��3����У�μ�ʵ����ε�ѧ����1200�ˣ����У�μ�D��ʵ����ε�ѧ����Լ�����ˣ�
��4��ѡ��D����ѧʵ�����ѧ������2��Ů����2���������ֳ�ɫ���ִ�4���������ȡ2����У����ƣ������б�����״ͼ��������ȡ������ǡ����1��Ů����1�������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������y��ax2��bx��c��ͼ����ͼ��ʾ����ô����x��һԪ���η���ax2��bx��c��3��0�ĸ�������ǣ� ��
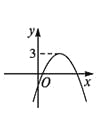
A. ����������ȵ�ʵ����
B. ��������ŵ�ʵ����
C. ��������ȵ�ʵ����
D. û��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��x2+bx+c��ֱ��y��![]() x��3���ڣ�B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
x��3���ڣ�B���㣬���е�A��y���ϣ���B����Ϊ����4����5������PΪy��������������һ���㣬����P��PC��x���ڵ�C����AB�ڵ�D��
��1���������߶�Ӧ�ĺ�������ʽ��
��2����O��A��P��DΪ�����ƽ���ı����Ƿ���������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��ѧ����綯����ѧ����ͨ��ȫ����������Ϊ�˽�ij��ѧ2500��ѧ���ҳ��ԡ���ѧ����綯����ѧ����̬�ȣ������������400���ҳ��������360���ҳ��ַ���̬�ȣ�������˵��������ǣ�������
A.���鷽ʽ�dz�������B.��Уֻ��360���ҳ��ַ���̬��
C.������400���ҳ��ԡ���ѧ����綯����ѧ����̬��D.��УԼ��90%�ļҳ��ַ���̬��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳��
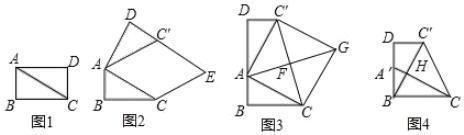
���ۺ���ʵ�����ϣ���ʦ��ͬѧ���ԡ�����ֽƬ�ļ�ƴ��Ϊ���չ��ѧ����� ͼ 1����������ֽƬ ABCD �ضԽ��� AC �������õ���ABC �͡�ACD���������� AB ��4cm��AC��8cm��
�������֣�
��1����ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת�Ϧ���ʹ�Ϧ�����BAC���õ���ͼ 2 ��ʾ�ġ�AC��D������ C �� AC���ƽ���ߣ��� DC'���ӳ��� ���ڵ� E�����ı��� ACEC�����״�� ��
��2������С�齫ͼ 1 �еġ�ACD �Ե� A Ϊ��ת���ģ�����ʱ�뷽����ת��ʹ B�� A��D ������ͬһ��ֱ���ϣ��õ���ͼ 3 ��ʾ�ġ�AC��D������ CC'��ȡ CC����� �� F������ AF ���ӳ����� G��ʹ FG��AF������ CG��C��G���õ��ı��� ACGC�䣬 �������������Σ�����֤��������ۣ�
ʵ��̽����
��3������С���ڴ���С�鷢�ֽ��۵Ļ����ϣ��������²���������ABC ���� BD ����ƽ�ƣ�ʹ�� B ��� A �غϣ���ʱ A ��ƽ���� A'�㣬A'C �� BC���ཻ�ڵ� H�� ��ͼ 4 ��ʾ������ CC�䣬���� tan��C��CH ��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com