
如图1是一个新款水杯,水杯不盛水时按如图2所示的位置放置,这样可以快速晾干杯底,干净透气;将图2的主体部分的抽象成图3,此时杯口与水平直线的夹角为35°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长(精确到0.1cm)
(参考数据sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002)

科目:初中数学 来源:2016年初中毕业升学考试(福建南平卷)数学(解析版) 题型:选择题
闽北某村原有林地120公顷,旱地60公顷,为适应产业结构调整,需把一部分旱地改造为林地,改造后,旱地面积占林地面积的20%,设把x公顷旱地改造为林地,则可列方程为( )
A.60﹣x=20%(120+x) B.60+x=20%×120
C.180﹣x=20%(60+x) D.60﹣x=20%×120
查看答案和解析>>
科目:初中数学 来源:2016届江西吉安二中等九校中考一模数学试卷(解析版) 题型:解答题
如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.

查看答案和解析>>
科目:初中数学 来源:2016年初中毕业升学考试(黑龙江绥化卷)数学(解析版) 题型:填空题
自主学习,请阅读下列解题过程.
解一元二次不等式: >0.
>0.
【解析】
设 =0,解得:
=0,解得: =0,
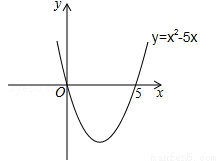
=0, =5,则抛物线y=
=5,则抛物线y= 与x轴的交点坐标为(0,0)和(5,0).画出二次函数y=
与x轴的交点坐标为(0,0)和(5,0).画出二次函数y= 的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即
的大致图象(如图所示),由图象可知:当x<0,或x>5时函数图象位于x轴上方,此时y>0,即 >0,所以,一元二次不等式
>0,所以,一元二次不等式 >0的解集为:x<0或x>5.
>0的解集为:x<0或x>5.
通过对上述解题过程的学习,按其解题的思路和方法解答下列问题:
(1)上述解题过程中,渗透了下列数学思想中的 和 .(只填序号)
①转化思想 ②分类讨论思想 ③数形结合思想
(2)一元二次不等式 <0的解集为 .
<0的解集为 .
(3)用类似的方法解一元二次不等式: >0.
>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com