
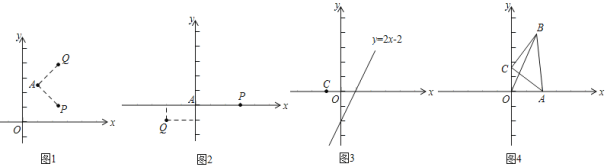
【题目】对于平面直角坐标系xOy中的点A和点P,若将点P绕点A逆时针旋转90°后得到点Q,则称点Q为点P关于点A的“垂链点”,图1为点P关于点A的“垂链点”Q的示意图.
(1)如图2,已知点A的坐标为(0,0),点P关于点A的“垂链点”为点Q;
①若点P的坐标为(3,0),则点Q的坐标为 ;
②若点Q的坐标为(﹣2,﹣1),则点P的坐标为 ;
(2)如图3,已知点C的坐标为(﹣1,0),点D在直线y=2x﹣2上,若点D关于点C的“垂链点”E在坐标轴上,试求出点D的坐标;
(3)如图4,在平面直角坐标系xOy,已知点A(2,0),点C是y轴上的动点,点A关于点C的“垂链点”是点B,连接BO、BA,则BO+BA的最小值是 .
【答案】(1)①(0,3);②(﹣1,2);(2)点D(﹣1,﹣4)或(![]() ,﹣1);(3)
,﹣1);(3)![]() .
.
【解析】
(1)①若点P的坐标为(3,0),则点Q的坐标为 (0,3),②若点Q的坐标为(﹣2,﹣1),同理可得:点P的坐标为(﹣1,2);
(2)分当点E(E′)落在x轴上、点E落在y轴两种情况,分别求解即可;
(3)BO+BA=![]()
![]()
,BO+BA的值,相当于求点P(m,m)到点M(1,﹣1)和点N(0,﹣1)的最小值,相当于在直线y=x上寻找一点P(m,m),使得点P到M(0,﹣1),到N(1,﹣1)的距离和最小,即可求解.
解:(1)①若点P的坐标为(3,0),则点Q的坐标为 (0,3),
故答案为:(0,3);
②若点Q的坐标为(﹣2,﹣1),
同理可得:点P的坐标为(﹣1,2),
故答案为:(﹣1,2);
(2)①当点E(E′)落在x轴上时,如图1
则点D(D′)关于点C的“垂链点”在x轴上,点CD⊥x轴,
x=﹣1时,y=﹣2﹣2=﹣4,
故点D(﹣1,﹣4);
②当点E落在y轴时,如图1:
设点D(m,2m﹣2),

点D的“垂链点E在y轴上,
过点D作DH⊥x轴于点H,
则△CHD≌△EOC(AAS),
则DH=OC=1,即:2m﹣2=﹣1,解得:m=![]() ,
,
故点D(![]() ,﹣1),
,﹣1),
综上,点D(﹣1,﹣4)或(![]() ,﹣1);
,﹣1);
(3)如图作BH⊥OH于H.
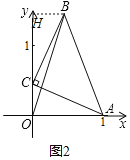
设点C的坐标为(0,m),
由(1)知:OC=HB=m,OA=HC=1,
则点B(m,1+m),
则:BO+BA=![]()
![]()
,
BO+BA的值,相当于求点P(m,m)到点M(1,﹣1)和点N(0,﹣1)的最小值,
相当于在直线y=x上寻找一点P(m,m),使得点P到M(0,﹣1),到N(1,﹣1)的距离和最小,
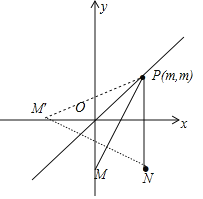
作M关于直线y=x的对称点M′(﹣1,0),
易知PM+PN=PM′+PN≥NM′,
M′N=![]() =
=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a≠0) 交x轴正半轴于点A,直线y=2x 经过抛物线的顶点M.已知该抛物线的对称轴为直线x=2,交x轴于点B.
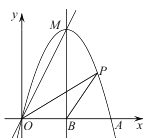
(1)求a,b的值;
(2)P是第一象限内抛物线上的一点,且在对称轴的右侧,连接OP,BP.设点P的横坐标为m ,△OBP的面积为S,![]() .求K关于m 的函数表达式及K的范围.
.求K关于m 的函数表达式及K的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大学生创业团队抓住商机,购进一批干果分装成营养搭配合理的小包装后出售,每袋成本3元.试销期间发现每天的销售量y(袋)与销售单价x(元)之间满足一次函数关系,部分数据如表所示,其中3.5≤x≤5.5,另外每天还需支付其他费用80元.

(1)请直接写出y与x之间的函数关系式;
(2)如果每天获得160元的利润,销售单价为多少元?
(3)设每天的利润为w元,当销售单价定为多少元时,每天的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
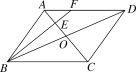
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
;②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中正确结论是_________.(把正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
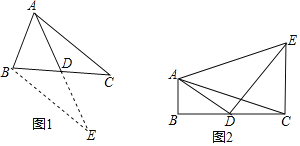
【题目】数学兴趣小组在活动时,老师提出了这样一个问题:如图1,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点,求BC边上的中线AD的取值范围.
,D是BC的中点,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使![]() ,请补充完整证明“
,请补充完整证明“![]() ≌
≌![]() ”的推理过程.
”的推理过程.
![]() 求证:
求证:![]() ≌
≌![]()
证明:![]() 延长AD到点E,使
延长AD到点E,使![]()
在![]() 和
和![]() 中
中![]() 已作
已作![]() ,
,
![]() ______
______![]() ,
,
![]() 中点定义
中点定义![]() ,
,
![]() ≌
≌![]() ______
______![]() ,
,
![]() 探究得出AD的取值范围是______;
探究得出AD的取值范围是______;
(感悟)解题时,条件中若出现“中点”“中线”等字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
(问题解决)
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,AD是
,AD是![]() 的中线,
的中线,![]() ,
,![]() ,且
,且![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
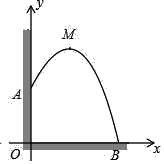
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与地面垂直).抛物线的最高点M离墙1m,离地面![]() m.
m.
(1)建立适当的平面直角坐标系,求抛物线的解析式.
(2)求水的落地点B与点O的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com