
科目:初中数学 来源: 题型:解答题
 如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.
如图,EF∥AD,∠1=∠2,∠BAC=87°,将求∠AGD的过程填写完整.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 甲乙两地相距400km,一辆轿车从甲地出发,以一定的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地(轿车的速度大于货车的速度),与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.两车之间的距离y(km)与轿车行驶的时间x(h)的函数图象如图.
甲乙两地相距400km,一辆轿车从甲地出发,以一定的速度匀速驶往乙地.0.5h后,一辆货车从乙地出发匀速驶往甲地(轿车的速度大于货车的速度),与轿车在途中相遇.此后,两车继续行驶,并各自到达目的地.两车之间的距离y(km)与轿车行驶的时间x(h)的函数图象如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.
如图,在△ABC中,O是BC上的点,⊙O经过A,B两点,与BC交于点E,D是下半圆的点,且OD⊥BC于点O,并连结AD交BC于点F,若AC是⊙O的切线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
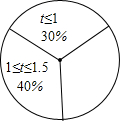 为了了解某初级中学800名学生完成课外作业所用的时间情况,从该校学生中随机抽取部分学生进行调查,按被调查学生完成课外作业时间t(小时)的人数分布,制成如图统计表和扇形统计图(均不完整)
为了了解某初级中学800名学生完成课外作业所用的时间情况,从该校学生中随机抽取部分学生进行调查,按被调查学生完成课外作业时间t(小时)的人数分布,制成如图统计表和扇形统计图(均不完整)| 时间t(小时) | t≤1 | 1<t≤1.5 | 1.5<t≤2 | t>2 |
| 人数(人) | 15 | 20 | 10 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com