
【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
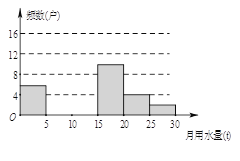
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
【答案】(1)抽样调查,50 (2)12,0.08 (3)72°(4)640户
【解析】试题分析:(1)由调查了小区部分家庭可知是抽样调查,根据0<x≤5中频数为6,频率为0.12,则调查总户数为6÷0.12=50,则样本容量为50;
(2)用样本容量×根据5<x≤10中频率0.12即可得m,用4÷样本容量即可得n,根据m 的值以及16补全统计图即可;
(3)用0.2乘以360度即可得;
(4)根据样本数据中超过10t的家庭数,即可得出1000户家庭超过10t的家庭数.
试题解析:(1)由随机调查了该小区部分家庭可知这是抽样调查,
根据0<x≤5中频数为6,频率为0.12,则样本容量为:6÷0.12=50,
故答案为:抽样调查,50;
(2)m=50×0.24=12,n=4÷50=0.08,
故答案为:12,0.08,
图形如下:

(3)月均用水量“![]() ”的圆心角的度数是360°×0.2=72°,
”的圆心角的度数是360°×0.2=72°,
故答案为:72°;
(4)1000×(0.32+0.20+0.08+0.04)=640户,
答:该小区月均用水量超过20t的家庭大约有640户.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程![]() =0的两个实数根.
=0的两个实数根.
(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=![]() ,求AC、BC的长.
,求AC、BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点![]() 分别在正方形
分别在正方形![]() 的边
的边![]() 上,
上, ![]() ,连接
,连接![]() ,则
,则![]() ,试说明理由.
,试说明理由.
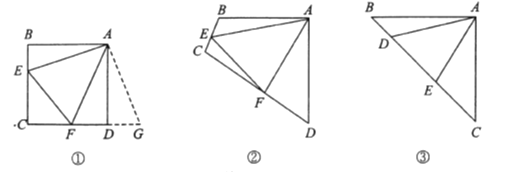
(1)思路梳理
因为![]() ,所以把
,所以把![]() 绕点
绕点![]() 逆时针旋转90°至
逆时针旋转90°至![]() ,可使
,可使![]() 与
与![]() 重合.因为
重合.因为![]() ,所以
,所以![]() ,点
,点![]() 共线.
共线.
根据 ,易证![]() ,得
,得![]() .请证明.
.请证明.
(2)类比引申
如图②,四边形![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,
上, ![]() .若
.若![]() 都不是直角,则当
都不是直角,则当![]() 与
与![]() 满足等量关系时,
满足等量关系时, ![]() 仍然成立,请证明.
仍然成立,请证明.
(3)联想拓展
如图③,在![]() 中,
中, ![]() ,点
,点![]() 均在边
均在边![]() 上,且
上,且![]() .猜想
.猜想![]() 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1;
(2)画出与△A1B1C1关于y轴对称的△A2B2C2;
(3)若点P(a,b)是△ABC边上任意一点,P2是△A2B2C2边上与P对应的点,写出P2的坐标为 ;
(4)试在y轴上找一点Q(在图中标出来),使得点Q到B2、C2两点的距离之和最小,并求出QB2+QC2的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=![]() .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,则下列结论:①DE=CD;②AD平分∠CDE;③∠BAC=∠BDE;④BE+AC=AB,其中正确的是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com