练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．计算（$\sqrt{12}$-$\sqrt{3}$）÷$\sqrt{3}$的结果是（　　）
    A．-1B．-$\sqrt{3}$C．$\sqrt{3}$D．1

    分析 先化简括号内的式子，然后合并同类项，再根据二次根式的除法即可计算出题目中式子的正确结果，本题得以解决．

    解答 解：（$\sqrt{12}$-$\sqrt{3}$）÷$\sqrt{3}$
    =$（2\sqrt{3}-\sqrt{3}）÷\sqrt{3}$
    =$\sqrt{3}÷\sqrt{3}$
    =1，
    故选D．

    点评 本题考查二次根式的混合运算，解题的关键是明确二次根式的混合运算的计算方法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．计算：
    （1）${（-\frac{1}{2}）^{-2}}-{（-1）^{2012}}×{（π-\sqrt{2}）^0}-\sqrt{{{（-4）}^2}}+\sqrt{25}$．
    （2）${（\sqrt{3}-\sqrt{2}）^2}+（\sqrt{3}+\sqrt{2}）（\sqrt{3}-\sqrt{2}）$
    （3）先化简，再求值：$（\frac{x^2}{x-1}-\frac{2x}{1-x}）÷\frac{x}{x-1}$，其中x=$\sqrt{3}+1$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列事件是必然事件的是（　　）
    A．在装有5个红球的袋中摸出1个球，是红球
    B．小麦的亩产量一定为1500千克
    C．打开电视机，正在转播足球比赛
    D．农历十五的晚上一定能看到圆月

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图是一个半圆形桥洞截面示意图，圆心为O，直径AB是河底线，弦CD是水位线，CD∥AB，且CD=24 m，OE⊥CD于点E．已测得sin∠DOE=$\frac{12}{13}$．
    （1）求AB的长；
    （2）根据需要，水面要以每小时0.5m的速度下降，则经过多长时间才能将水排干？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．若关于x的方程3x-（2a-3）=5x+（3a+6）的解是负数，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（3$\sqrt{3}$+2$\sqrt{2}$）（3$\sqrt{3}$-2$\sqrt{2}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．下列各式中，能用平方差公式进行计算的是（　　）
    A．（-x-y）（x+y）B．（2x-y）（y-2x）C．（1-$\frac{1}{2}$x）（-1-$\frac{1}{2}$x）D．（3x+y）（x-3y）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．类似于平面直角坐标系，如图1，在平面内，如果原点重合的两条数轴不垂直，那么我们称这样的坐标系为斜坐标系．若P是斜坐标系xOy中的任意一点，过点P分别作两坐标轴的平行线，与x轴、y轴交于点M、N，如果M、N在x轴、y轴上分别对应的实数是a、b，这时点P的坐标为（a，b）．
    （1）如图2，在斜坐标系xOy中，画出点A（-2，3）；
    （2）如图3，在斜坐标系xOy中，已知点B（5，0）、C（0，4），且P（x，y）是线段CB上的任意一点，则y与x之间的等量关系式为y=-$\frac{4}{5}$x+4；
    （3）若（2）中的点P在线段CB的延长线上，其它条件都不变，试判断（2）中的结论是否仍然成立，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

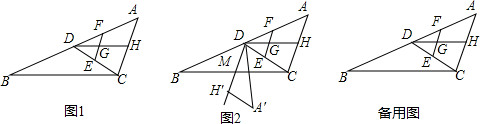    14．如图1，在△ABC中，CD为AB边上的中线，点E、F分别在线段CD、AD上，且$\frac{DF}{DB}=\frac{DE}{DC}$．点G是EF的中点，射线DG交AC于点H．
    （1）求证：△DFE∽△DAC；
    （2）请你判断点H是否为AC的中点？并说明理由；
    （3）若将△ADH绕点D顺时针旋转至△A′DH′，使射线DH′与射线CB相交于点M（不与B，C重合．图2是旋转后的一种情形），请探究∠BMD与∠BDA′之间所满足的数量关系，并加以证明．

    查看答案和解析>>

    同步练习册答案