
【题目】定义:三角形一边上的点将该边分为两条线段,且这两条线段的积等于这个点到该边所对顶点连线的平方,则称这个点为三角形该边的“好点”.如图1,△ABC中,点D是BC边上一点,连结AD,若![]() ,则称点D是△ABC中BC边上的“好点”.
,则称点D是△ABC中BC边上的“好点”.
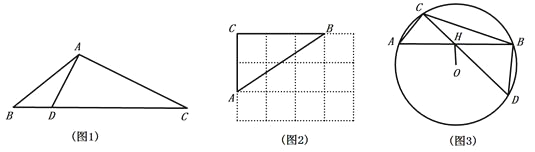
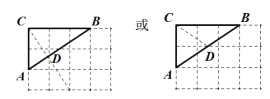
(1)如图2,△ABC的顶点是![]() 网格图的格点,请仅用直尺画出AB边上的一个“好点”.
网格图的格点,请仅用直尺画出AB边上的一个“好点”.
(2)△ABC中,BC=9,![]() ,
,![]() ,点D是BC边上的“好点”,求线段BD的长.
,点D是BC边上的“好点”,求线段BD的长.
(3)如图3,△ABC是![]() 的内接三角形,OH⊥AB于点H,连结CH并延长交
的内接三角形,OH⊥AB于点H,连结CH并延长交![]() 于点D.
于点D.
①求证:点H是△BCD中CD边上的“好点”.
②若![]() 的半径为9,∠ABD=90°,OH=6,请直接写出
的半径为9,∠ABD=90°,OH=6,请直接写出![]() 的值.
的值.
【答案】(1)详见解析;(2)![]() 或5;(3)①详见解析;②
或5;(3)①详见解析;②![]() .
.
【解析】
(1)作AB边上的垂线或中线即可;
(2)作AE⊥BC于点E,根据三角函数求出BE、CE、AE的长,设DE为a,分①若点D在点E左侧②若点D在点E右侧,根据“好点”的定义进行求解即可;
(3)①根据“同弧或等弧所对的圆周角相等”证△AHC∽△DHB,再根据“好点”的定义判断即可;
②连接AD,根据∠ABD=90°判断AD为直径,用勾股定理求出AH的长,再根据勾股定理求出DH的长,根据①中的结论求出CH的长即可求得比值.
(1)如图所示:D点及为AB边上的“好点”
(2)作AE⊥BC于点E,由![]() ,
,![]() 可设AE=4x,
可设AE=4x,
则BE=3x,CE=6x,
∴BC=9x=9,∴![]() ,
,
∴BE=3,CE=6,AE=4,
设DE=a,
①若点D在点E左侧,
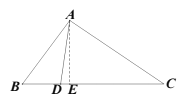
由点D是BC边上的“好点”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() .
.
②若点D在点E右侧,
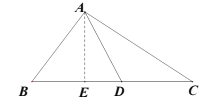
由点D是BC边上的“好点”知,![]() ,
,
∴![]() ,即
,即![]() ,
,
解得![]() ,
,![]() (舍去)
(舍去)
∴![]() .
.
∴![]() 或5.
或5.
(3)①∵∠CHA=∠BHD,∠ACH=∠DBH
∴△AHC∽△DHB
∴![]() ,即
,即![]()
∵OH⊥AB
∴AH=BH
∴![]()
∴点H是△BCD中CD边上的“好点”.
②连接AD.
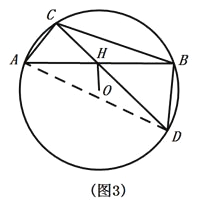
∵∠ABD=90°
∴AD为直径,
∵OH⊥AB,OH=6
∴![]() ,BD=2OH=12
,BD=2OH=12
∴BH=AH=![]()
∴![]()
由①得:![]()
即![]()
∴CH=![]()
∴![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
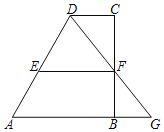
【题目】如图,四边形ABCD中,AB∥CD,CD≠AB,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:CFFG=DFBF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=12,EF=8,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)一个不透明的口袋中装有2个红球(记为红球1、红球2)、1个白球、1个黑球,这些球除颜色外都相同,将球摇匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出1个球,再从余下的3个球中任意摸出1个球,请用列举法(画树状图或列表)求两次都摸到红球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题呈现)阿基米德折弦定理:
如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
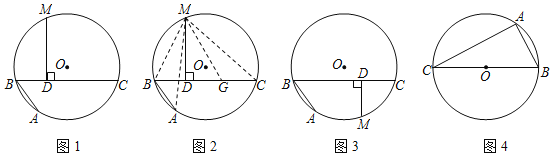
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是![]() 的中点,
的中点,
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程,分别写出下列步骤的理由:
① ,
② ,
③ ;
(理解运用)如图1,AB、BC是⊙O的两条弦,AB=4,BC=6,点M是![]() 的中点,MD⊥BC于点D,则BD= ;
的中点,MD⊥BC于点D,则BD= ;
(变式探究)如图3,若点M是![]() 的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
(实践应用)根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=6,⊙O的半径为5,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
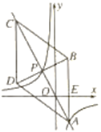
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的对角线AC与BD交于点P(-1,2),AB⊥x轴于点E,正比例函数y=mx的图像与反比例函数![]() 的图像相交于A,P两点。
的图像相交于A,P两点。
(1)求m,n的值与点A的坐标;
(2)求证:![]() ∽
∽![]()
(3)求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的两个图形
中的两个图形![]() 与
与![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为图形
为图形![]() 上任意一点,如果
上任意一点,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 间的“和睦距离”,记作
间的“和睦距离”,记作![]() ,若图形
,若图形![]() 有公共点,则
有公共点,则![]() .
.
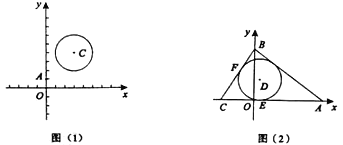
(1)如图(1),![]() ,
,![]() ,⊙
,⊙![]() 的半径为2,则
的半径为2,则![]() ,
,![]() ;
;
(2)如图(2),已知![]() 的一边
的一边![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() .
.
①![]() 是
是![]() 内一点,若
内一点,若![]() 、
、![]() 分别且⊙
分别且⊙![]() 于E、F,且
于E、F,且![]() ,判断
,判断![]() 与⊙
与⊙![]() 的位置关系,并求出
的位置关系,并求出![]() 点的坐标;
点的坐标;
②若以![]() 为半径,①中的
为半径,①中的![]() 为圆心的⊙
为圆心的⊙![]() ,有
,有![]() ,
,![]() ,直接写出
,直接写出![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是等腰Rt△ABC的外接圆,点D是![]() 上一点,BD交AC于点E,若BC=4,AD=
上一点,BD交AC于点E,若BC=4,AD=![]() ,则AE的长是( )
,则AE的长是( )
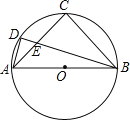
A. 1 B. 1.2 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
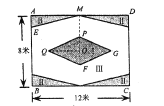
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=75°,BC=7,△ABC的面积为14,D为 BC边上一动点(不与B,C重合),将△ABD和△ACD分别沿直线AB,AC翻折得到△ABE与△ACF,那么△AEF的面积最小值为_____.
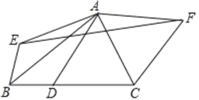
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com