
����Ŀ��������̽�� ̽��������ͼ1��ͼ3�У���ABC�����Ϊa ��
��1����ͼ1, �ӳ���ABC�ı�BC����D��ʹCD=BC������DA������ACD�����ΪS1����S1=________���ú�a�Ĵ���ʽ��ʾ����




��2����ͼ2���ӳ���ABC�ı�BC����D���ӳ���CA����E��ʹCD=BC��AE=CA������DE������DEC�����ΪS2����S2= ���ú�a�Ĵ���ʽ��ʾ����
��3����ͼ2�Ļ������ӳ�AB����F��ʹBF=AB������FD��FE���õ���DEF����ͼ3��������Ӱ���ֵ����ΪS3����S3=__________���ú�a�Ĵ���ʽ��ʾ����
���֣�����������������ABC���߾�˳���ӳ�һ�����������ö˵㣬�õ���DEF����ͼ3������ʱ�����dz���ABC������չ��һ�Σ����Է��֣���չһ�κ�õ�����DEF�������ԭ����ABC�����_____����
���𰸡���1��a����2��2a����3��6a��7.
��������(1)���ݵȵȸߵ������������Ƚ��;(2)�ֱ��A��E��BD�Ĵ���,������������λ�߶����������ε������ʽ��⼴��;(3)�ɡ�BFD����ECD����AEF�ı߳�Ϊ��ABC�߳���һ��,�����AEF�ĸ���Ƚ��.
��:(1) ��CD=BC, ��ABC�����Ϊa, ��ABC���ACD�ĸ����,![]() ;
;
(2)�ֱ��A��E��AG��BD,EF��BD,G��FΪ����,
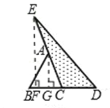
��AG��EF,��AΪCE���е�,![]() ,
,
��BC=CD,![]() ;
;
(3) �ߡ�BDF�ı߳�BD�ǡ�ABC�߳�BC��2��,�������ε�����Ϊ��һ���������ߵ��ӳ���,![]() ,�ߡ�ABC�����Ϊa,
,�ߡ�ABC�����Ϊa,![]() .ͬ���ɵ�,
.ͬ���ɵ�,![]() ,
,![]() ,
,![]() .
. ![]() ,
,![]() ,
,![]() ,
,
����չһ�κ�õ��ġ�DEF�������ԭ����ABC�����7��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
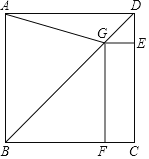
����Ŀ����ͼ����������ABCD�У���G�ڶԽ���BD��![]() �����
�����![]() �غ�
�غ�![]() �ڵ�
�ڵ�![]() �ڵ�F������AG��
�ڵ�F������AG��
![]() д���߶�
д���߶�![]() ����֮���������ϵ����˵�����ɣ�
����֮���������ϵ����˵�����ɣ�
![]() ��������ABCD�ı߳�Ϊ
��������ABCD�ı߳�Ϊ![]() �����߶�BG�ij���
�����߶�BG�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���E��P�ڱ�AB�ϣ���AE=BP������E��P��BC��ƽ���ߣ��ֱ�AC�ڵ�F��Q���ǡ�AEF�����ΪS1 �� �ı���EFQP�����ΪS2 �� �ı���PQCB�����ΪS3 �� 
��1����֤��EF+PQ=BC��
��2����S1+S3=S2 �� ��![]() ��ֵ��
��ֵ��
��3����S3��S1=S2 �� ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��1��0����B��0��-1����C��-1��2����D��2��-1����E��4��2������㣬������y=a��x-1��2+k��a��0���������е������㣮
��1����֤��C��E���㲻����ͬʱ��������y=a��x-1��2+k��a��0���ϣ�
��2����A��������y=a��x-1��2+k��a��0������Ϊʲô��
��3����a��k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
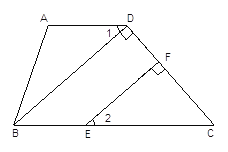
����Ŀ����ͼ�����ı���ABCD�У���A=104�㣭��2����ABC=76�㣫��2��BD��CD��D��EF��CD��F��
��֤����1=��2�������������֤�����̣�
֤������Ϊ��A��104�㣭��2����ABC��76�㣫��2���� ��
���� ��A����ABC��104�㣭��2��76�㣫��2�� �� ��ʽ���� ��
�� ��A����ABC��180��
���� AD��BC���� ��
���� ��1����DBC���� ��
��Ϊ BD��DC��EF��DC���� ��
���� ��BDC=90��,��EFC=90��,( )
���� ��BDC=��EFC,
���� BD�� ���� ��
���� ��2����DBC���� ��
���� ��1����2 �� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AB=2��E��AD����һ�㣨��E���A��D���غϣ���BE�Ĵ�ֱƽ���߽�AB��M����DC��N��
��1����AE=x���ı���ADNM�����ΪS��д��S����x�ĺ�����ϵʽ��
��2����AEΪ��ֵʱ���ı���ADNM�����������ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ͷ��13 800Ԫ�ʽ��ס������ֿ�Ȫˮ��500�䣬��Ȫˮ�ijɱ��ۺ����ۼ������ʾ��
���/���� | �ɱ��� | ���ۼ�(Ԫ/��) |
�� | 24 | 36 |
�� | 33 | 48 |
(1)���̳������ס������ֿ�Ȫˮ�������䣿
(2)ȫ������500���Ȫˮ�����̳�������������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������ABCD�У���E��O��F�ֱ�ΪAB��AC��AD���е㣬����CE��CF��OE��OF��
��1����֤����BCE�ա�DCF��
��2����AB��BC����ʲô��ϵʱ���ı���AEOF�������Σ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��A��B�������Ϸֱ��ʾ������a��b��A��B�����ľ����Ϊ|AB|��O��ʾԭ�㣮��A��B��������һ����ԭ��ʱ���������AΪԭ�㣬��ͼ1����|AB|=|OB|=|b|=|a-b|����A��B���㶼����ԭ��ʱ��
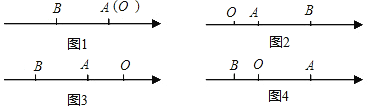
����ͼ2������A��B����ԭ����ұ�ʱ��|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|��
����ͼ3������A��B����ԭ������ʱ��|AB|=|OB|-|OA|=|b|-|a|=-b-��-a��=|a-b|��
����ͼ4������A��B��ԭ�������ʱ��|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|��
�ش��������⣺
��1������������������A��B�����ľ���Ϊ|AB|=______��
��2���������ϵĵ�A��ʾ����Ϊ3����B��ʾ����Ϊ-4����A��B�����ľ���Ϊ______��
��3���������ϵĵ�A��ʾ����Ϊx����B��ʾ����Ϊ-2����|AB|=______����|AB|=3����x��ֵΪ______��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com